Fonte: Shutterstock.
Deseja ouvir este material?
Áudio disponível no material digital.
sem medo de errar
A situação-problema da seção apresenta um contexto de metrologia e qualidade na área agrícola. Você, como analista de dados, ficou responsável por dar suporte em um estudo para a utilização de reagentes em defensivos naturais, considerando as variáveis Preço/Litro, Rendimento (L/ha) e Custo/ha. Para a seleção do reagente, você ficou responsável por simular dois gráficos de controle, um com amplitude de quatro desvios padrão (dois para cima e dois para baixo) e outro com seis desvios padrão (três para cima e três para baixo). Um gráfico de controle apresenta três elementos principais: uma linha representando a média, um limite superior de controle e um limite inferior de controle. Com base no conjunto de dados informados, o primeiro passo é encontrar as médias e os desvios padrão das variáveis de interesse. Como olharemos para a variável “Custo/ha” para a tomada de decisão, apresentaremos somente seus respectivos cálculos. No intuito de facilitar a operação, é sugerida a construção da Tabela 2.13.
Tabela 2.13 | Suporte de cálculo das medidas-resumo
Fonte: elaborada pelo autor.
| Produto | Preço/litro | Rendimento (L/ha) | Custo/ha |
|---|---|---|---|
| 1 | R$ 51,00 | 4,93 | R$ 251,43 |
| 2 | R$ 56,00 | 5,69 | R$ 318,64 |
| 3 | R$ 90,00 | 3,07 | R$ 276,30 |
| 4 | R$ 150,00 | 6,21 | R$ 931,50 |
| 5 | R$ 109,00 | 8,6 | R$ 937,40 |
| 6 | R$ 165,00 | 3,38 | R$ 557,70 |
| 7 | R$ 25,00 | 8,6 | R$ 215,00 |
| 8 | R$ 39,00 | 5,45 | R$ 212,55 |
| 9 | R$ 58,00 | 12,44 | R$ 721,52 |
| 10 | R$ 70,00 | 6,77 | R$ 473,90 |
| 11 | R$ 44,00 | 6,98 | R$ 307,12 |
| 12 | R$ 48,00 | 5,19 | R$ 249,12 |
| 13 | R$ 75,00 | 4,95 | R$ 371,25 |
| 14 | R$ 55,00 | 3,65 | R$ 200,75 |
| 15 | R$ 78,00 | 4,65 | R$ 339,30 |
| Total | R$ 1.113,00 | R$ 90,26 | R$ 6.363,48 |
| Média | R$ 74,20 | R$ 6,02 | R$ 424,23 |
| Variância | 1.588,74 | 5,97 | 63.224,90 |
| Desvio padrão | 39,86 | 2,44 | 251,45 |
Com todas as informações reunidas, podemos iniciar o cálculo dos limites estabelecidos. Para tanto, teremos duas simulações:
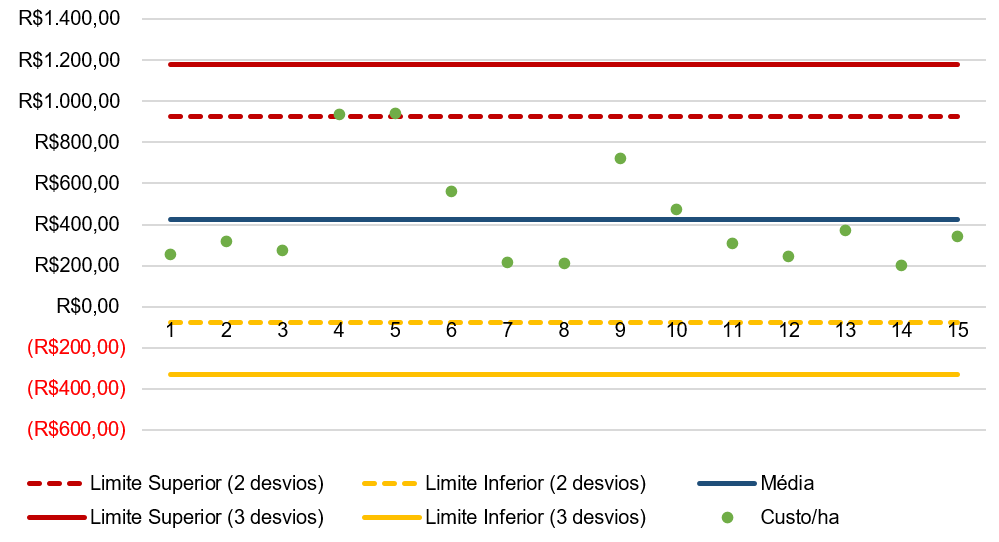
É possível construirmos um gráfico de controle, como na Figura 2.3.
Observamos que dos quinze reagentes avaliados, somente o 4 e 5 não se enquadram nos limites de controle, considerando o limite de dois desvios. Para três, no entanto, nenhum reagente ficou fora dos limites. O que aconteceria se alterássemos o cálculo dos limites para somente um desvio padrão?
Avançando na prática
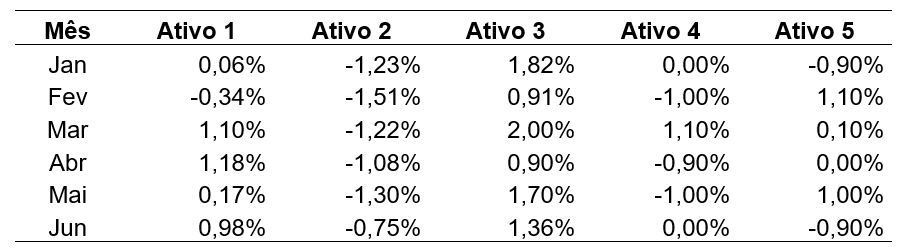
Você trabalha para uma empresa de investimentos e ficou responsável por elaborar uma análise para um cliente, considerando opções de investimento. Ao fechar o contrato, o cliente deixou claro que gostaria de um investimento com uma média de retorno positiva e menor variância, considerando os seis últimos meses de análise. Você elencou cinco opções de investimento que se enquadram nos critérios solicitados pelo cliente. Os rendimentos mensais dos ativos estão expressos na Tabela 2.14.
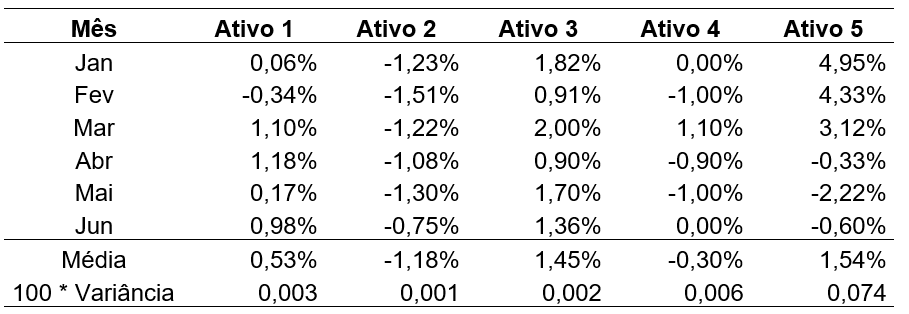
Para a resolução da situação-problema, devemos calcular as médias e os desvios padrão dos cinco ativos elencados, considerando os seis meses de observação. Como se trata de valores percentuais, é sugerida a multiplicação do valor da variância por uma constante, que pode ser 100. Serão obtidos os valores da média e variância, conforme a Tabela 2.15.
Seguindo o padrão desejado pelo cliente, a melhor opção de investimento é o Ativo 3, que apresenta a maior média de retorno e a menor variância. O Ativo 5 poderia ser uma boa opção, pois apresenta uma alta média de retorno. No entanto, devido a sua alta variância, há indícios de que, embora o retorno possa ser alto, situações de perda também podem ocorrer. Se considerássemos somente uma das medidas apresentadas, por exemplo, a variância, poderíamos cair na armadilha de indicar o Ativo 2, que possui o menor valor associado. No entanto, o mesmo ativo tem a menor média de retorno. Por essa razão, é importante reforçar que as medidas de localização e de dispersão devem ser utilizadas em conjunto.