
Fonte: Shutterstock.
Deseja ouvir este material?
Áudio disponível no material digital.
Praticar para aprender
Prezado estudante, nesta seção encerraremos o conteúdo das medidas-resumo, que compõe um dos mais importantes conjuntos de ferramentas para a análise de dados. Para tanto, trabalharemos com as medidas relativas à distribuição, mais precisamente, com os quantis.
Os quantis são medidas utilizadas em diversas áreas de análise, como investimentos, saúde e RH, entre outros, e são capazes de oferecer informações valiosas a respeito de um conjunto de dados, como concentração de valores e características da distribuição.
Por essa razão, iniciamos a seção trazendo a importância da utilização dessas medidas, bem como a forma de cálculo para sua obtenção. Em seguida, tratamos dos principais quantis, também denominados quantis notáveis, como decis, percentis e quartis. Fixados esses conceitos, trabalharemos com um dos mais importantes gráficos da estatística e probabilidade: o boxplot.
Assim como nas seções anteriores, buscamos trabalhar os conceitos teóricos e desenvolver um conteúdo prático, que permite uma melhor fixação dos elementos mais importantes da seção. Por essa razão, você encontrará o desenvolvimento dos exercícios na linguagem R, o que permitirá simular um contexto do cotidiano de análise de dados.
Ao término desta seção e, consequentemente, da unidade, você vai dominar as principais medidas-resumo e será capaz de realizar análises exploratórias de dados.
Você é gerente de vendas de uma empresa que tem doze lojas no estado de São Paulo, nove no estado do Rio de Janeiro e onze em Minas Gerais. Após os fechamentos anuais de vendas, você dispõe de dados suficientes para realizar um relatório e irá prepará-lo com informações como média, mediana e quartis. No entanto, o diretor empresa deseja ter essa visualização separada por estado e, se possível, em um único slide. As vendas foram distribuídas conforme a Tabela 2.16:
| Lojas | São Paulo | Rio de Janeiro | Minas Gerais |
|---|---|---|---|
| 1 | R$ 49.899 | R$ 34.444 | R$ 16.357 |
| 2 | R$ 47.101 | R$ 26.223 | R$ 13.303 |
| 3 | R$ 44.777 | R$ 41.194 | R$ 15.715 |
| 4 | R$ 25.721 | R$ 41.846 | R$ 16.569 |
| 5 | R$ 42.555 | R$ 22.262 | R$ 20.199 |
| 6 | R$ 29.781 | R$ 14.354 | R$ 18.904 |
| 7 | R$ 42.641 | R$ 30.757 | R$ 16.428 |
| 8 | R$ 35.982 | R$ 39.891 | R$ 20.444 |
| 9 | R$ 34.953 | R$ 33.098 | R$ 27.301 |
| 10 | R$ 26.302 | NA | R$ 24.687 |
| 11 | R$ 46.122 | NA | R$ 27.493 |
| 12 | R$ 48.999 | NA | NA |
Realize as análises, considerando as medidas apresentadas.
Uma excelente seção. Bons estudos!
conceito-chave
Nas seções anteriores, trabalhamos dois conjuntos de medidas de grande relevância para a análise da dados: medidas de posição (média, mediana e moda) e medidas de dispersão (amplitude, variância e desvio-padrão, entre outras). Entretanto, na presença de pontos discrepantes, essas medidas são altamente sensíveis. Além disso, nos ajudam a compreender o comportamento central e a dispersão de determinado conjunto de dados, porém pouco informam a respeito de sua distribuição (BUSSAB; MORETTIN, 2017).
Nesse sentido, trazemos, nesta seção, algumas medidas que nos permitem obter alguns padrões de comportamento em termos de distribuição de dados. Quando trabalhamos, por exemplo, com as médias, obtemos informações a respeito do comportamento central de um conjunto. Da mesma forma, quando diante de uma medida de dispersão, obtemos insights a respeito da variação de um conjunto de dados. Nesse sentido, por mais que essas informações sejam de grande relevância, não temos indicativos de padrões de distribuição desses conjuntos. Por isso, é de grande importância explorarmos tais medidas.
O principal conceito envolvido quando discutimos as medidas de distribuição é o quantil, expresso por . A letra representa uma proporção de determinado conjunto de dados, de modo que . Nesse sentido, quando , por exemplo, estamos dividindo um conjunto de dados em 2 partes iguais, considerando o total de observações.
O termo quantil é expresso genericamente. Ao dividirmos um conjunto de dados em quatro intervalos regulares, configura-se o termo quartil, que representa, portanto, a quarta parte de uma distribuição, conforme expresso na Figura 2.4.

Observamos, portanto, a presença de três pontos, que formarão quatro quartis. Em q(0,25), denominado primeiro quartil, temos 25% dos dados da distribuição à esquerda e 75% à direita. Em q(0,50), o segundo quartil, temos 50% para cada lado. Por fim, no terceiro quartil, em que q=0,75, temos 75% dos dados à esquerda e 25% à direita.
Assimile
Note que o segundo quartil divide a amostra em dois grupos iguais quanto ao número de observações. Esse é o mesmo conceito de uma importante medida de localização, a mediana. Logo, obter o segundo quartil de um conjunto de dados é a mesma coisa que obter sua mediana.
Da mesma forma, se dividirmos uma distribuição em dez intervalos regulares, obteremos decis, ou seja, grupos que concentram 10% das observações cada um, conforme apresentado na Figura 2.5.
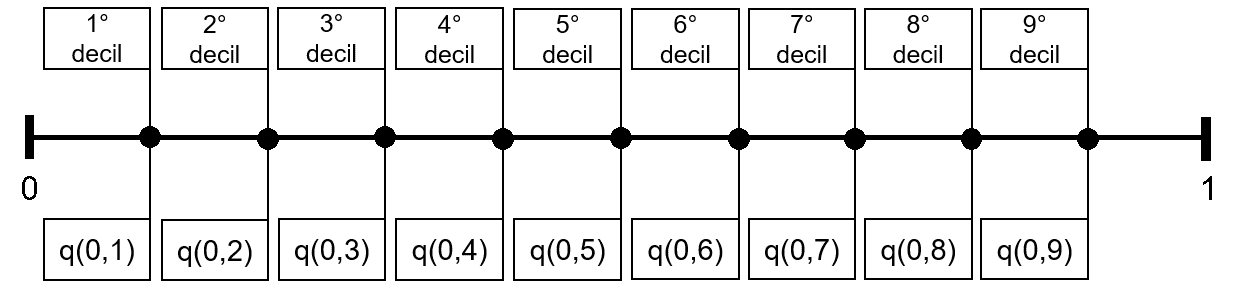
Além dos quartis e decis, é bem comum serem utilizados os percentis, principalmente quando se trabalha com maiores conjuntos de dados. De forma análoga, um percentil representa a centésima parte regular de uma distribuição.
É importante destacar que os quantis podem assumir diferentes nomes e representar o mesmo conjunto, como nos casos a seguir:
Em relação ao cálculo dos quantis, não existe um padrão definido. O R, por exemplo, possui nove formas distintas de se obter os respectivos valores. Para o desenvolvimento desta seção, utilizaremos o seguinte estimador para cálculo:
Dessa forma, o valor do quantil equivale ao elemento da posição de número . Suponha que uma empresa está avaliando o perfil etário de seus quinze colaboradores. Após realizar um levantamento, foram obtidas as seguintes idades: 23,19, 22, 23, 25, 28, 58, 34, 47, 39, 42, 45, 35, 32, 62. O primeiro passo para a obtenção dos quantis é elencar as observações de forma crescente. Realizada essa etapa, obteremos o conjunto ordenado: {19, 22, 23, 23, 25, 28, 32, 34, 35, 39, 42, 45, 47, 58, 62}.
Considerando as idades dos funcionários, vamos calcular o segundo quartil (q(0,5)) de nosso conjunto, cujo valor, como vimos, equivale à mediana. Substituindo p=0,5 e n=15 na fórmula para cálculo do quantil, temos que
Como o oitavo número do conjunto de dados ordenado é 34, . Neste caso, o valor é um número inteiro, ou seja, conseguimos encontrar facilmente a posição do respectivo valor do quantil. Nos casos em que os valores posicionais são decimais, devemos realizar uma média ponderada entre os dois elementos vizinhos. É o que acontece, por exemplo, quando calculamos , que nos apresenta um índice . Logo, observamos que o sexto decil do nosso conjunto de dados equivale ao elemento da posição de número 9,6, ou seja, algum valor entre a nona e a décima observação.
Nesse caso, precisaremos realizar uma média ponderada. Com o auxílio da Figura 2.6, podemos perceber que 9,6 está mais próximo de 10 do que de 9. Então, atribuiremos o peso 0,6 à décima observação e 0,4 à nona observação.

Considerando os pesos atribuídos, o cálculo de é expresso por:
Nesta situação, o valor de está mais próximo da posição imediatamente superior. Por essa razão, atribuímos um peso maior à observação da décima posição, em detrimento da nona. No entanto, se tivéssemos uma situação contrária, deveríamos ter cuidado para atribuir os pesos corretamente.
Suponha que agora desejamos calcular , ou seja, o quarto decil de nosso conjunto de dados. Aplicando a fórmula para a obtenção do quantil, temos que:
Com o auxílio da Figura 2.7, observamos que nosso índice está mais próximo de 6 do que de 7. Por essa razão, devemos atribuir um maior peso à sexta observação.

Desse modo, o cálculo de é dado por:
Para o caso geral, seja o valor referente à posição imediatamente anterior a e o valor referente à posição imediatamente posterior. Então, para encontrarmos o valor do quantil considerando a ponderação, devemos aplicar a seguinte fórmula:
A princípio a fórmula parece um pouco confusa, mas vamos por partes. Quando trabalhamos com , obtemos que . Dessa forma, a posição imediatamente anterior equivale a 9, e a imediatamente posterior é equivalente a 10. Além disso, sabemos que o nono elemento do nosso conjunto é 35 e o décimo é 39 . Pronto, já dispomos de todos os elementos necessários para o cálculo de . Substituindo os valores, temos que:
De modo análogo, para , . Assim, , , e . Aplicando a fórmula, temos que:
Perceba, portanto, que esses são exatamente os mesmos valores obtidos anteriormente.
Além da regra para o caso geral, destacamos duas propriedades importantes: se , então . Da mesma forma, se , então . Como exemplo, considerando o mesmo conjunto de idades dos beneficiários da empresa, . Pelo fato de o número de observações ser igual a 15, não é possível encontrar . Assim, . Por outro lado, para , temos que . Dessa forma, como a posição mínima é a de número 1, .
Com base nos exemplos apresentados, podemos construir a seguinte relação para o cálculo dos quantis:
No contexto das medidas baseadas na distribuição, uma importante ferramenta é o boxplot, utilizado em diversos contextos de análise. O boxplot, ou diagrama de caixas, é um gráfico que nos permite obter informações a respeito dos quartis de um conjunto de dados e de pontos possíveis pontos discrepantes, também denominados outliers.
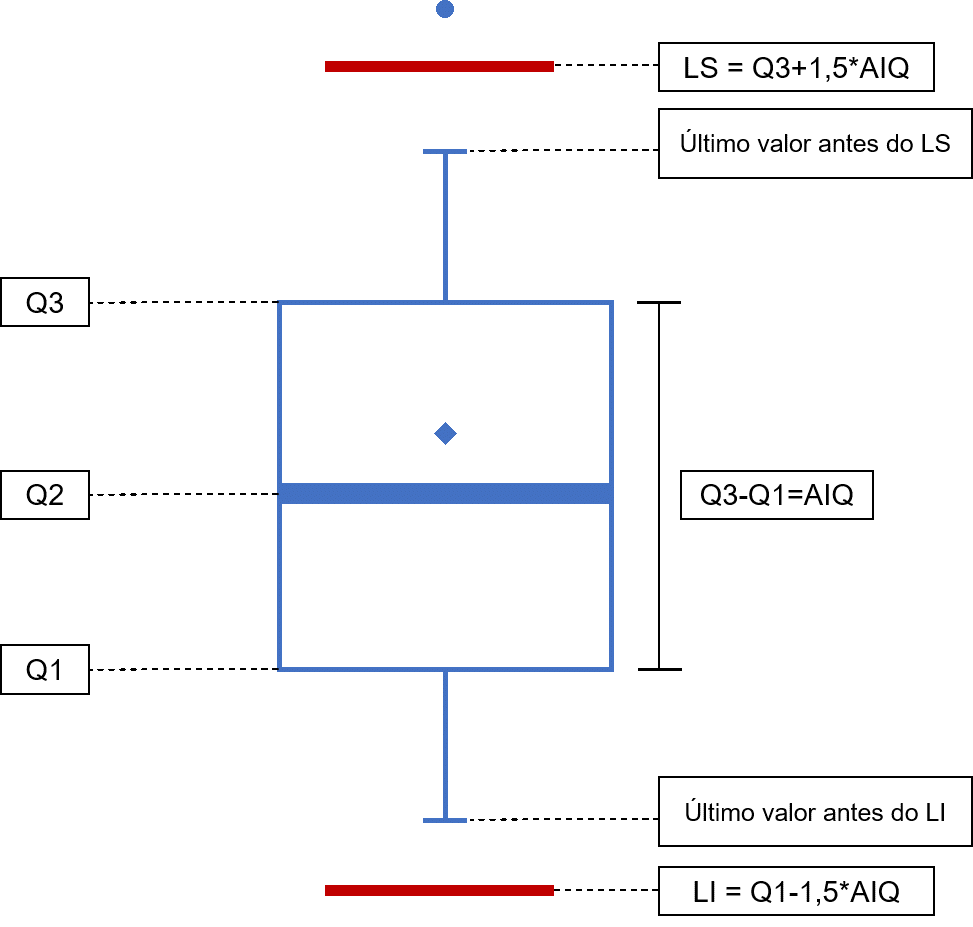
Com base na Figura 2.8, podemos observar que o boxplot apresenta alguns elementos principais:
- Q1, Q2 e Q3 representam, respectivamente, o primeiro, segundo e terço quartis do conjunto de dados.
- A barra horizontal, que coincide com o segundo quartil, representa, também, a mediana das observações.
- A Amplitude (ou distância) Interquartil (AIQ) é obtida por . Além de representar o tamanho da caixa, a AIQ é utilizada para o cálculo dos limites superior (LS) inferior (LI).
- O losango, geralmente interno à caixa, representa a média das observações. É um item opcional, nem sempre apresentado no gráfico.
- O pequeno círculo localizado além do LS é um possível ponto discrepante, que também pode estar presente abaixo do LI. Nem todo conjunto de dados apresentará observações fora dos limites. Em casos de ocorrência, é necessário realizar alguns testes estatísticos, como o Teste de Grubbs, para a confirmar se a observação fora dos limites realmente se trata de um ponto discrepante.
Nesse sentido, podemos destacar as seguintes estruturas do boxplot:
- Caixa principal, delimitada por Q1 e Q3 e dividida internamente por Q2 (mediana).
- Losango (opcional): ponto indicativo da média do conjunto de dados.
- Bigodes (ou whisker): retas verticais externas à caixa. Indicam o maior valor anterior ao LS e última observação antes do LI.
- Círculos: nem sempre estarão presentes, dependendo do conjunto de dados. Representam possíveis pontos discrepantes.
Também é bem comum os boxplots serem apresentados de forma horizontal, o que não muda a interpretação. Basicamente, é realizado um giro de 90°, no sentido horário, alterando a visualização, conforme disposto na Figura 2.9.
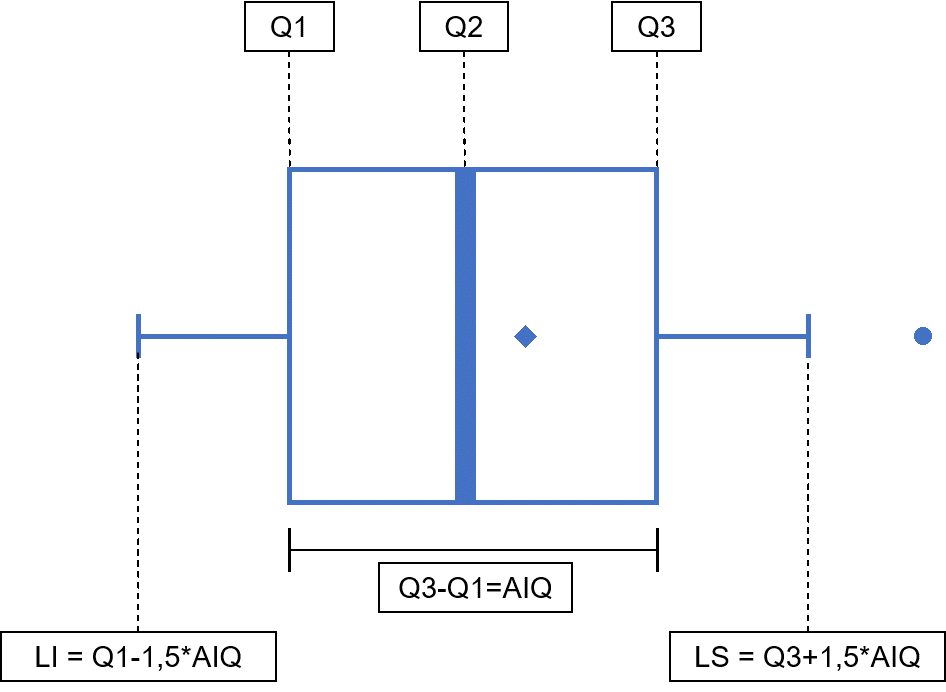
a mediana é equivalente a 34, ou seja, . Dessa forma, para construirmos um boxplot, devemos calcular Q1, Q3 e a média dos dados (opcional). Para o cálculo de Q1, temos que:
Q3, por sua vez, é obtido por:
Com base nos quartis encontrados, podemos sumarizar os valores conforme a Figura 2.10.

Aplicando o cálculo da média, obteremos que:
Além disso, a Amplitude Interquartil é dada por:
Assim, podemos obter os limites superior e inferior:
Reflita
Como estamos trabalhando com idade, um limite inferior de dez anos certamente não faz sentido. Já sabemos, portanto, que não teremos pontos discrepantes abaixo desse limite. No entanto, manteremos o valor para a construção do gráfico.
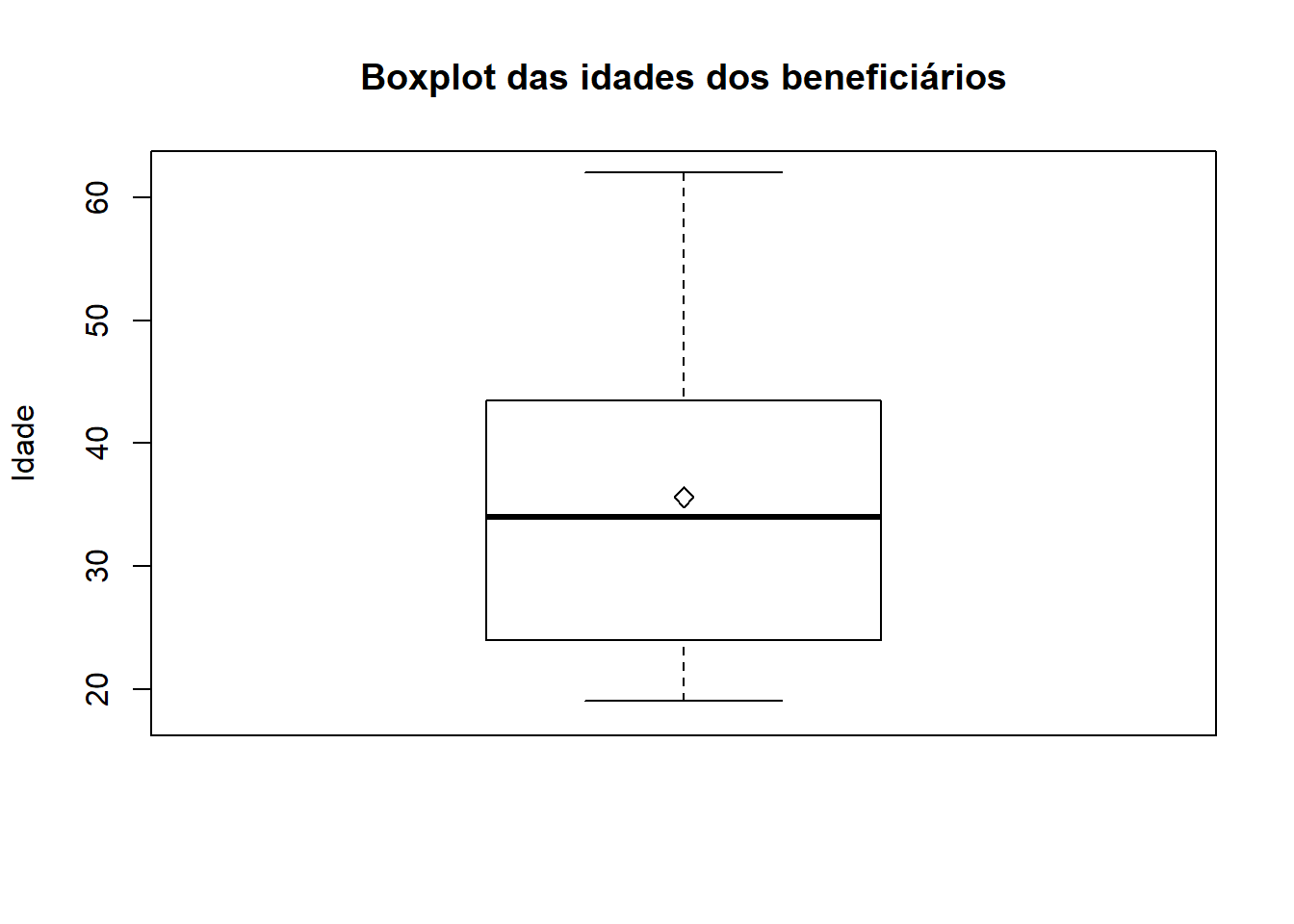
Os valores respectivos aos bigodes são 62 (maior valor antes do LS) e 19 (último valor antes do LI). Assim, dispomos de todos os elementos necessários para elaborarmos o boxplot, apresentado na Figura 2.11.
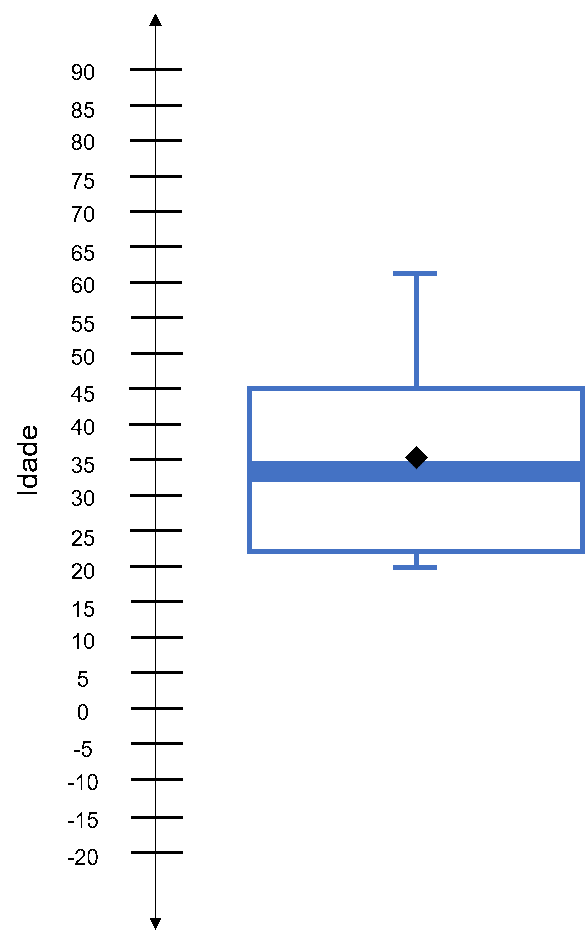
Notamos, portanto, que nosso conjunto de dados não apresenta observações candidatas a pontos discrepantes. Observa-se, também, que a média e a mediana estão próximas, mas que apresentam valores distintos, possivelmente em função da idade equivalente a 62 anos, que acaba por puxar levemente o valor da média para cima, mas não o da mediana.
Exemplificando
Na atividade prática de análise de dados, é muito comum trabalharmos com comparações entre boxplots, no intuito de observar os padrões de comportamento entre grupos distintos. Nessas situações, colocamos os boxplots lado a lado e avaliamos fatores como quartis, tamanho das caixas, medianas e possíveis pontos discrepantes, entre outros. Então, temos uma situação semelhante à observada na Figura 2.12:

Nenhuma das marcas apresenta possíveis candidatos a pontos discrepantes. Além disso, a mediana de insatisfação da Marca C é superior à da Marca B que, por sua vez, é maior do que a Marca A. A maior variação se encontra na Marca C, posto que a caixa apresenta grande amplitude interquartil. A menor variação está na Marca B. Olhando somente para os boxplots, há indícios de que a Marca A gera menos insatisfação do que as demais.
Após fixarmos a construção do boxplot, trabalharemos de forma prática, por meio da linguagem R. Para tanto, utilizaremos os mesmos valores de idades, que nos permitirá comparar os valores e avaliar se o método default de cálculo que o R utiliza é o mesmo que desenvolvemos durante o corpo do texto.
Medidas Baseadas na Distribuição
Prezado estudante, nesta seção trabalharemos as medidas de dispersão e a representação gráfica por meio do boxplot. Para tanto, utilizaremos o exemplo das idades dos beneficiários de uma empresa, apresentado no corpo do texto da seção. Para retomarmos, o conjunto apresenta quinze observações, dispostas, ordenadamente, da seguinte forma: 19, 22, 23, 23, 25, 28, 32, 34, 35, 39, 42, 45, 47, 58, 62.
Como nas seções anteriores, o primeiro passo será criar o conjunto de dados no R, utilizando o comando c().

Vamos obter os quantis de p=0,4p=0,4 e p=0,6p=0,6. Para tanto, utilizamos o comando quantile().

Em seguida, trabalharemos para a obtenção dos quartis do conjunto de dados. Para tanto, podemos utilizar o mesmo comando quantile() ou o summary(), que também apresenta os quartis, junto com outras medidas resumo.
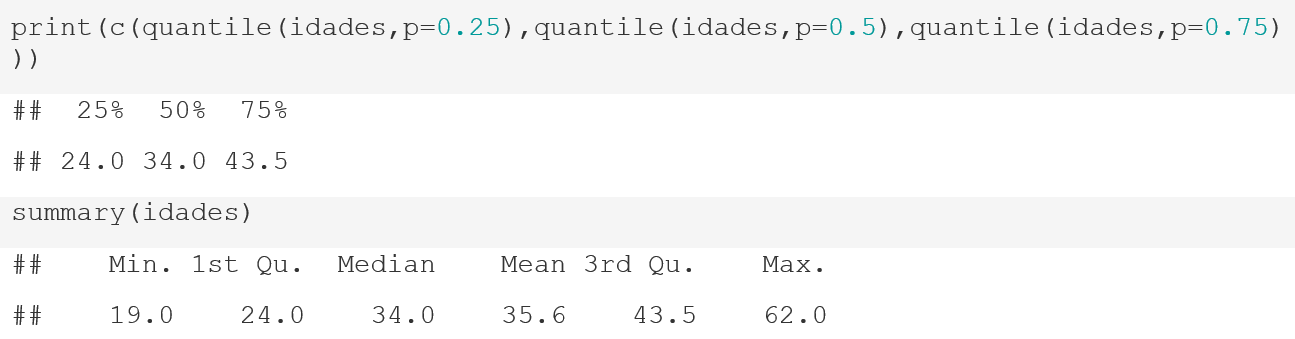
Obtidos os quartis, realizaremos o comando boxplot(), que nos trará os gráficos solicitados.

Para realizarmos o boxplot por meio do pacote ggplot2, devemos apresentar os seguintes comandos:


Para visualizar o vídeo, acesse seu material digital.
Encerramos, portanto, mais um importante conteúdo em Probabilidade e Estatística para Análise de Dados. Os tópicos abordados nesta seção são bastante comuns no dia a dia de um profissional de dados. O boxplot é uma ferramenta amplamente utilizada e difundida na área, e permite reunir diversas informações da distribuição em um só lugar.
Faça a valer a pena
Questão 1
Os quantis são intervalos regulares de um conjunto de dados, ou seja, dividem uma distribuição em grupos com o mesmo número de observações, elencados de forma crescente.
Considerando o contexto, avalie as afirmativas a seguir:
- O segundo quartil de um conjunto é equivalente à mediana.
- O segundo quartil de um conjunto é equivalente ao quinto decil.
- O segundo quartil de um conjunto é equivalente quinquagésimo percentil.
- O segundo quartil de um conjunto é equivalente média.
Considerando o contexto apresentado, está correto o que se afirma em:
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Correto!
A questão apresenta a conceituação de quantis e solicita o domínio do entendimento relacionado a quartis. O segundo quartil é dado por , valor equivalente à mediana. Olhando para decis, é equivalente ao quinto decil. Ao se avaliar em termos percentis, observa-se que se trata do quinquagésimo percentil. Por essa razão, as afirmativas I, II e III estão corretas. A alternativa IV apresenta um erro conceitual, ao passo que o segundo quartil representa a mediana, em vez da média de um conjunto de dados.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Questão 2
Uma empresa está avaliando o tempo que seus funcionários gastam no trajeto entre suas casas e o trabalho. Com base em um levantamento, foi obtida a seguinte relação, expressa em minutos de deslocamento e apresentada na tabela a seguir:
| Quantil | Tempo de deslocamento |
|---|---|
| 1º decil | 10 minutos |
| 2º decil | 18 minutos |
| 1º quartil | 21 minutos |
| 2º quartil | 32 minutos |
| 3º quartil | 66 minutos |
Com base nas informações apresentadas, assinale a alternativa que apresenta o tempo máximo gasto por metade dos beneficiários da empresa.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Correto!
A questão apresenta um contexto de aplicação dos quantis. A metade de um conjunto de dados também é conhecida pela mediana, ou seja, segundo quartil. Nesse sentido, a alternativa que apresenta o valor máximo gasto por metade dos funcionários da empresa é 2º quartil – 32 minutos.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Questão 3
Uma corretora de investimentos está avaliando dois ativos para indicar a seus clientes. Para tanto, a empresa dispõe de um boxplot, com os retornos diário dos ativos nos últimos doze meses, conforme expresso na figura que segue.
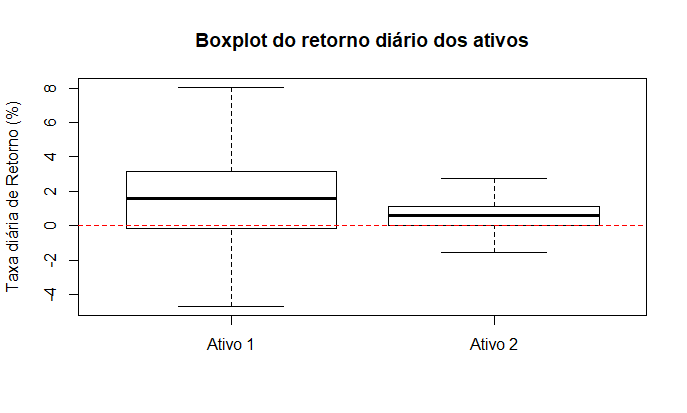
Com base nas informações apresentadas, assinale a alternativa correta.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Correto!
A questão exige o domínio da estrutura de um boxplot, bem como dos conceitos relacionados a quantis. Avaliando-se o gráfico, é possível perceber que a mediana do Ativo 1, representada pela linha horizontal interna à caixa, está mais distante de zero que do Ativo 2. Além disso, o Ativo 2 apresenta valores mais concentrados, o que lhe confere tanto uma caixa, quanto bigodes menores. Avaliando-se os bigodes das caixas, é possível observar que o Ativo 1 apresenta retornos máximos maiores do que o Ativo 2. Além disso, ao se olhar, novamente, para as linhas horizontais internas às caixas, é possível observar que a mediana do Ativo 1 é matematicamente superior à mediana do Ativo 2. Por fim, quando se observa os limites das caixas, é possível perceber que o terceiro quartil do Ativo 1 está acima do terceiro quartil do Ativo 2. Por essa razão, a afirmativa verdadeira é: O terceiro quartil do Ativo 1 é matematicamente superior ao terceiro quartil do Ativo 2.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
REFERÊNCIAS
BUSSAB, W. de O.; MORETTIN, P. A. Estatística básica. São Paulo: Saraiva, 2017.
SCHNEIDER, H.; DA SILVA, C. A. O uso do modelo box plot na identificação de anos-padrão secos, chuvosos e habituais na microrregião de Dourados, Mato Grosso do Sul. Revista do Departamento de Geografia, v. 27, p. 131-146, 2014.



