lorem ipsum dolor sit amet
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nunc dignissim euismod urna tincidunt sagittis. Vivamus id vehicula eros, non scelerisque eros.

Fonte: Shutterstock.
Praticar para aprender
Caro aluno
Nesta seção, desenvolveremos tópicos teóricos importantes para formação em análise de dados. Iniciaremos a discussão abordando a distinção entre os termos margem de erro, erro, nível de confiança e intervalo de confiança que, apesar de diferentes entre si, são frequentemente confundidos.
Em seguida, introduziremos dois métodos de reamostragem de grande utilização: Jackknife e Bootstrap. Aprenderemos a realizar o processo de amostragem, ainda que de forma simples, e a calcular os parâmetros desencadeados. Além desses dois métodos, também apresentaremos brevemente a Validação Cruzada e o Synthetic Minority Oversampling Technique (SMOTE), ferramentas de grande utilização na Inteligência Artificial, expressamente o Machine Learning.
Por fim, como estamos prestes a encerrar mais uma unidade, buscaremos, por meio de uma atividade prática no R, resgatar os principais conteúdos abordados nas seções anteriores, como o Teorema do Limite Central e as distribuições de dados. Nesse sentido, trabalhamos com alguns exemplos que permitam observar como as médias amostrais de uma distribuição de dados quaisquer possuem um comportamento com tendência à normalidade (TLC) e como os parâmetros das distribuições afetam em seus formatos. Para tanto, simulamos dados para quatro distribuições (duas discretas e duas contínuas). Fique à vontade para alterar os valores dos parâmetros e observar os impactos nas distribuições.
Assim como nas seções anteriores, é de grande importância que todos os recursos disponibilizados nesta seção sejam explorados, como as Situações-problema, as questões, o material complementar, entre outros. Eles o ajudarão a melhor fixar os conteúdos e o prepararão para caminharmos mais alguns passos em sua formação.
Caro aluno, a atividade de análise de dados apresenta diversos desafios em seu dia a dia, o que a faz ainda mais interessante. Frequentemente, deparamo-nos com situações que nos tiram de uma zona de conforto e nos fazem buscar formas de resolver problemas. Algo comum, por exemplo, é a limitação operacional em situações que envolvem populações com um grande número de observações. Como proceder uma análise de dados de uma empresa com 20.000, 30.000 ou até 100.000 funcionários? Ou, então, como realizar uma pesquisa eleitoral que indique as intenções de votos dos habitantes de um país? É preciso entrevistar cada um deles para que se obtenha um número representativo? A resposta é não! E é nesse sentido que se encaixa o importante conceito na análise de dados: a amostragem.
Outro tópico de grande relevância na análise de dados é análise de distribuição. O que faz, por exemplo, um conjunto de dados possuir um comportamento semelhante a um sino, na denominada distribuição normal? Ou em que contexto utilizamos uma distribuição t de Student? A compreensão desses conceitos é fundamental para que se avance em análises ainda mais interessantes, como o cálculo dos intervalos de confiança, a comparação estatística de médias, entre outras. Dessa forma, dominar tanto o processo de amostragem, quanto a análise de distribuição é de suma importância para a resolução de problemas práticos da atividade de análise de dados.
Você trabalha em uma empresa de pesquisa no agronegócio e está realizando um estudo a respeito do preço da saca de soja no Estado do Paraná. Para tanto, foi coletada uma amostra com 10 observações do preço da saca em uma semana específica. Os dados obtidos estão apresentados na Tabela 3.8.
| Observação | Preço da Saca |
|---|---|
| 1 2 3 4 5 6 7 8 9 10 |
167,79 162,11 163,65 153,18 164,58 161,36 160,70 156,11 161,24 169,58 |
No intuito de obter um parâmetro de viés do preço médio dessa amostra, você deverá realizar uma reamostragem bootstrap, considerando cinco novas amostras aleatórias, e avaliar qual é o valor do viés para esses conjuntos de dados.
Uma ótima seção e um excelente aprendizado!
conceito-chave
Quando trabalhamos com modelos de Probabilidade e Estatística, é comum nos deparamos com situações que envolvem os conceitos de erro e intervalo de confiança. Nas seções anteriores, foram discutidos brevemente esses conceitos, precisamente, margem de erro e nível de confiança, destacando que se trata de tópicos diferentes, mas frequentemente confundidos.
O erro estatístico é caracterizado pelo desvio de uma observação predita em relação a seu valor real. Suponha, por exemplo, que estamos trabalhando com um modelo de regressão linear dado por , em que se busca entender qual é o impacto da variável X na variável Y. A análise nos trará uma reta de regressão, que está representada em vermelho na Figura 3.13, Cada uma das bolinhas azuis são os valores reais de y, ou seja, as observações que já possui antes de realizar a análise. O erro relacionado a essas observações é dado pela diferença entre o valor estimado por meio da reta de regressão e o valor real de cada observação yi, ou seja, o erro trata da diferença entre o valor estimado e o valor real da observação.
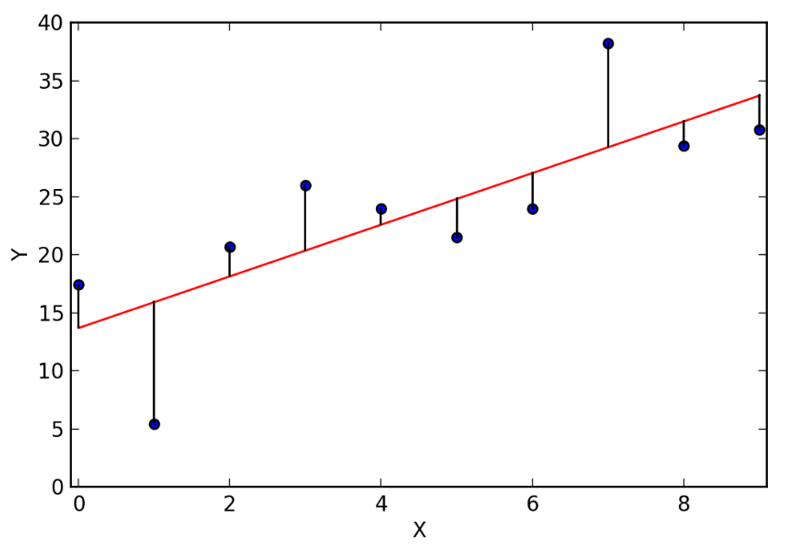
Na Figura 3.13, de forma visual, é possível identificar os erros por meio das barras verticais que ligam cada uma das observações da variável y com a reta de regressão em vermelho. A ideia de erro, portanto, é relativamente simples: trata-se da diferença entre o valor real e o valor calculado.
Reflita
Todos os erros vêm do mesmo lugar? Em análises de dados, frequentemente observa-se erros que impactam diretamente o resultado final de uma modelagem. Pode haver erros provenientes do processo de registro de dados, como uma vírgula colocada no lugar errado ou um número digitado incorretamente. Quando se trabalha com entrevistas, também é comum obter-se informações equivocadas por parte dos entrevistados, como o faturamento de uma empresa, o número de funcionários, total de idas ao médico, enfim, informações que muitas vezes as pessoas não possuem de prontidão, mas as apresentam como uma aproximação, que pode, de fato, estar errada. Se está trabalhando, por exemplo, com uma pesquisa de tamanho de mercado e é informado um número de clientes ou faturamento errado, possivelmente se apresentará uma estimativa subestimada (valor abaixo daquilo que realmente é) ou superestimada (valor acima daquilo que realmente é). Por essa razão, sempre que estiver diante de informações possivelmente equivocadas, é importante, quando possível, buscar revisitar as fontes de dados, no intuito de validar a veracidade da coleta.
Sanados esses diversos problemas possíveis, entra-se em uma questão de modelagem. Como profissionais de análise de dados, será sempre buscada a utilização de um modelo mais apropriado ao nosso conjunto de dados, o que, ainda assim, certamente gerará erros. Esses erros provenientes de modelagens são relativamente comuns, afinal foram construídos a partir de uma generalização e não especificamente para o conjunto de dados. É necessário, portanto, buscar modelos em que o erro seja o menor possível.
Entretanto, o erro nem sempre é fácil de ser encontrado. Isto porque o valor de um parâmetro populacional é frequentemente desconhecido. Suponha, por exemplo, que se está trabalhando com uma pesquisa eleitoral, entrevistando um conjunto de indivíduos que compõem uma amostra. Essa amostra nos trará um percentual de votos para o candidato A e outro percentual de votos para o candidato B. No entanto, não é sabido, ao certo, qual o percentual de toda a população, o que impede de calcular um erro estatístico preciso.
Por esta razão, em situações como esta, trabalha-se com o conceito de margem de erro, que permite inferir que o valor real da população está em alguma posição, por exemplo, de até 2% acima ou 2% abaixo do valor encontrado para a amostra.
A margem de 2%, por sua vez, está associada a um nível de confiança que, de modo geral, assegura que a cada 100 repetições de um experimento, em 95 delas o parâmetro populacional estará inscrito dentro dessa margem de erro, considerando um nível de confiança de 95%. Para um nível de confiança de 99%, 99 das 100 repetições apresentariam um resultado dentro dessa margem de erro. Para melhor compreensão, segue um exemplo:
Exemplificando
Um instituto de pesquisa está realizando uma pesquisa eleitoral, considerando uma população de 5.000 pessoas. Para tanto, foram entrevistados 400 indivíduos, de onde se obteve que 52% votariam no candidato A e 48% no candidato B. Dessa forma, temos que e , que são parâmetros amostrais.
Considerando que se está trabalhando com uma distribuição amostral, temos, que 95% das observações estão incluídas em um intervalo . Por mais que não se conheça os parâmetros populacionais p e , é sabido que 95% dos possíveis valores de estão dentro do intervalo . Assim, temos que: .
Como não se tem os parâmetros populacionais, devem ser feitas as seguintes ponderações: o desvio padrão populacional será substituído pelo erro padrão de e utiliza-se o valor de como aproximação de p, porém com uma margem de erro associada.
Para encontrar o erro padrão, segue a seguinte estrutura:
Nesse sentido, com 95% de confiança (valor que veio do intervalo ), tem-se que o intervalo de confiança da pesquisa eleitoral para a amostra selecionada é dado por
Considerando o parâmetro inicial obtido , a margem de erro é de 5 pontos percentuais (5 para cima e 5 para baixo).
Tem-se, portanto, os conceitos de nível de confiança (95%), intervalo de confiança ([47%; 57%]) e margem de erro (5%).
É muito comum, no entanto, estar diante de distribuições que não obedecem a uma regra de parametrização normal, ou seja, não possuem tendência à normalidade, com parâmetros e . Nesses casos, uma alternativa é proceder com métodos de reamostragem, que permitirão obter, a partir de uma amostra inicial, algumas informações de precisão e intervalo de confiança. Existem diversos métodos de reamostragem, porém nos atentemos a dois deles em específico: Bootstrap e Jackknife.
O Bootstrap é um método que consiste, de modo geral, da reamostragem com reposição de uma amostra inicial, com o objetivo de avaliar o desempenho da estimativa de um parâmetro , que pode ser, por exemplo, a média, desvio padrão, variância, entre outros parâmetros. Dessa forma, a partir de um conjunto X, com Xj observações independentes, criam-se outros t conjuntos de dados, denominados amostras bootstrap, com o mesmo número de observações da amostra inicial. O processo é representado pela Figura 3.14.
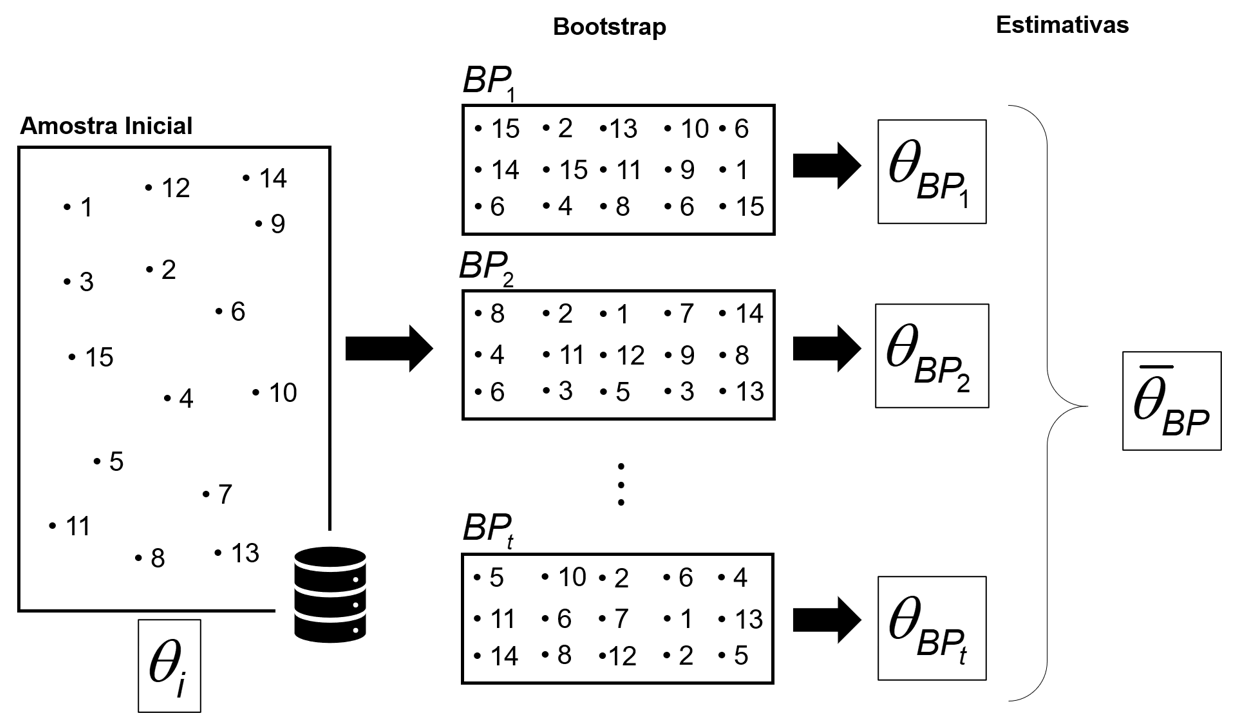
Essas t amostras gerarão t estimativas do parâmetro , que comporão uma média geral das amostras bootstrap, dada por .
Suponha, por exemplo, que se está diante de uma amostra com 10 observações, cuja média inicial é de 5,90. A partir desse conjunto, são geradas outras 5 amostras, a partir de um sorteio aleatório com reposição, conforme apresentado na Tabela 3.9. Cada um desses conjuntos, denominados amostras bootstrap, possuem uma média distinta. A média de BP 1, por exemplo, é de 6,10, enquanto a média do BP 3 equivale a 5,40.
| Observação | Amostra inicial | BP 1 | BP 2 | BP 3 | BP 4 | BP 5 |
|---|---|---|---|---|---|---|
| 1 2 3 4 5 6 7 8 9 10 |
3 10 6 9 2 5 4 10 3 7 |
7 9 5 10 3 5 10 5 5 2 |
9 10 2 10 9 7 2 3 7 3 |
7 5 3 6 3 6 9 5 6 4 |
6 10 10 2 4 3 2 9 7 10 |
7 4 6 7 2 5 10 2 10 6 |
| Média | 5,90 | 6,10 | 6,20 | 5,40 | 6,30 | 5,90 |
A partir dessas novas amostras geradas, é calculado o valor médio de suas respectivas médias e compara-se com a amostra inicial. No exemplo em questão, trabalha-se com a média, porém é possível trabalhar com outro parâmetro qualquer, denominado . Dessa forma, tem-se que:
Ao se comparar ao valor da amostra inicial , temos que a . Este valor de 0,08 é chamado viés amostral obtido por meio de bootstrap.
Outro método de reamostragem é o Jackknife (canivete, traduzido para o português). O método também é conhecido por leave-one-out, ao passo que são criadas novas amostras deixando-se sempre, ao menos, um elemento de fora. Suponha que se esteja trabalhando com uma amostra de 5 elementos e que desejamos obter a média geométrica desse conjunto de dados. Os valores das observações são apresentados na Tabela 3.10:
| Observação | 1 | 2 | 3 | 4 | 5 | Média Geométrica |
|---|---|---|---|---|---|---|
| Amostra Inicial | 12 | 15 | 13 | 11 | 15 | 13,10 |
A partir da aplicação do método de Jackknife, são criadas 5 novas amostras, com quatro elementos cada. Em seguida, obtém-se as respectivas médias geométricas e calcula-se a média aritmética desses 5 desvios encontrados. O procedimento nos dará o resumo de dados conforme a Tabela 3.11.
| Observação | 1 | 2 | 3 | 4 | 5 | Média Geométrica |
|---|---|---|---|---|---|---|
| Amostra Inicial | 12 | 15 | 13 | 11 | 15 | 13,10 |
| Jackknife 1 Jackknife 2 Jackknife 3 Jackknife 4 Jackknife 5 |
NA 12 12 12 12 |
15 NA 15 15 15 |
13 13 NA 13 13 |
11 11 11 NA 11 |
15 15 15 15 NA |
13,39 12,67 13,13 13,69 12,67 |
| Média Aritmética (5 amostras Jackknife) | 13,11 | |||||
Dessa forma, obtém-se que a média geométrica da amostra inicial é de 13,10, enquanto a média geométrica (média aritmética das cinco médias geométricas obtidas) equivale a 13,11. A ideia é, portanto, criar uma melhor estimativa para o parâmetro analisado.
Assimile
Um outro tipo de reamostragem é a Validação Cruzada, amplamente utilizada na construção de modelos de Machine Learning. De forma geral, esse tipo de reamostragem é utilizado para validar o desempenho preditivo de um algoritmo, ou seja, a capacidade de classificar um vetor de dados corretamente, de acordo com uma característica de interesse. A validação cruzada funciona da seguinte forma: suponha que um conjunto de dados tenha 1.000 observações. Reserva-se um percentual desses dados para treinar o algoritmo e utiliza-se o restante para testar o desempenho desse treinamento. Repete-se esse processo por k vezes e obtém-se, ao final, um desempenho médio desses k grupos . A ideia, no entanto, é que, nesse conjunto de k grupos, todas as observações são utilizadas para teste e todas são utilizadas para treino ao menos uma vez, conforme apresentado na Figura 3.15.
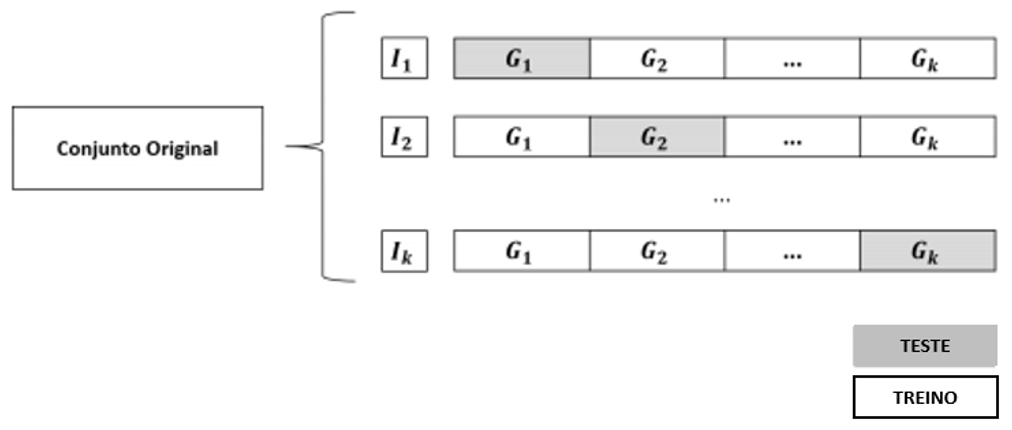
Nesse sentido, quando k=4, temos uma parte ((1/4)=25%) destinada ao teste do algoritmo, e o restante ((3/4)=75%) destinado ao treinamento. Quando k=10, teremos, portanto, um percentual de teste de 1/10=10% e de 9/10=90% para treino. Esse é um método em que, ao final da análise, teremos testado o desempenho do algoritmo em 100% dos dados. Por esse razão, sua utilização é amplamente difundida pelos profissionais de Machine Learning.
São compreendidos, portanto, os dois principais métodos de reamostragem presentes na Estatística. Existem outras formas para a realização da reamostragem, principalmente ligadas a aplicações de Machine Learning. Caso deseje conhecer um pouco mais, é apresentada uma breve discussão no Material Complementar desta seção.
Como encerramento desta unidade, resgatam-se alguns conceitos trabalhados nas duas seções anteriores, buscando trazer uma abordagem prática às situações apresentadas, principalmente aquelas relacionadas às distribuições de dados.
Esta seção prática está dividida em duas partes. Na primeira, desenvolve-se uma simulação para compreensão um pouco maior sobre o Teorema do Limite Central. Na segunda, foi trabalhado com duas distribuições discretas e duas distribuições contínuas, no intuito de compreender o que acontece quando alteramos seus respectivos parâmetros. Fique à vontade para alterar os parâmetros e avaliar os impactos causados na distribuição.
Teorema do Limite Central
Na primeira seção desta unidade, vimos que o Teorema do Limite Central enuncia que a média ou soma de variáveis aleatórias e independentes tendem a uma distribuição normal, independente do tipo de distribuição que essas variáveis possuem. A partir de então, simularemos duas distribuições, obter diferentes amostras a partir delas e verificar que a distribuição da média dessas amostras possui um comportamento com tendência à normalidade.
O primeiro passo é criar nosso conjunto de dados e, a partir dele, gerar novas amostras aleatórias. No primeiro exemplo, criaremos um conjunto por meio de uma distribuição normal, com n=10.000n=10.000 e, μ=15μ=15 e σ=3σ=3.
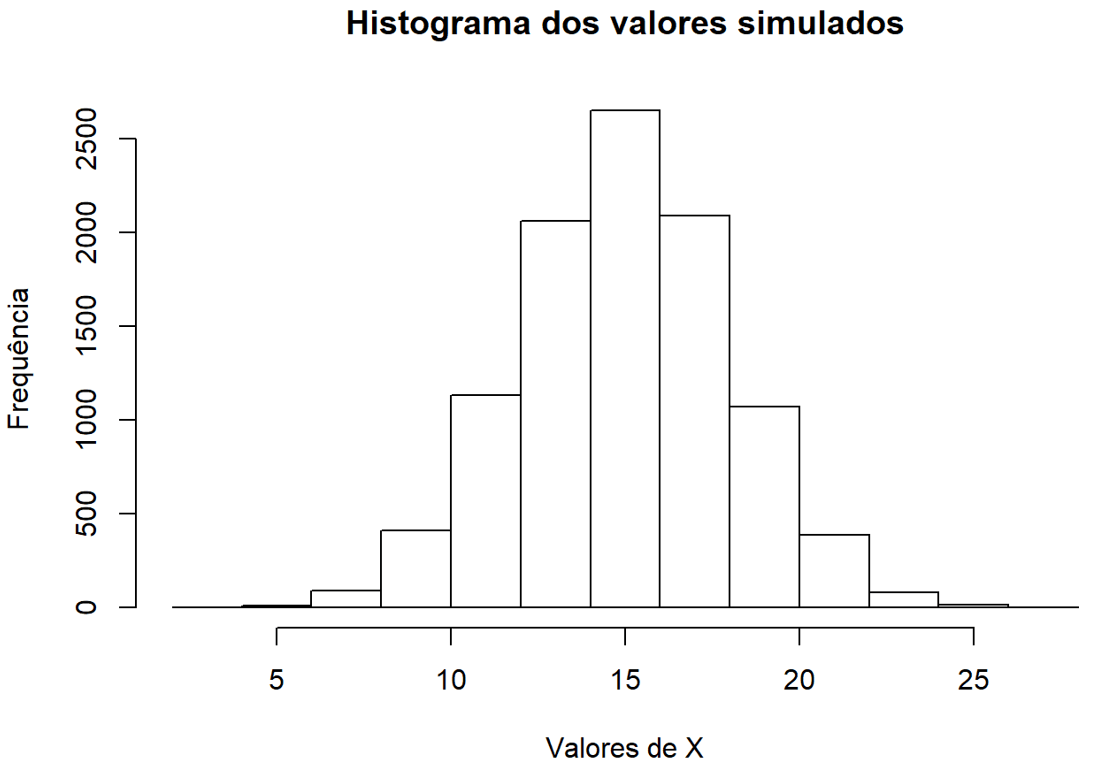
Criado o conjunto, iremos gerar, a partir dele, 1.000 amostras de 30 observações cada. Além disso, plotaremos o histograma do valor dessas médias amostrais.
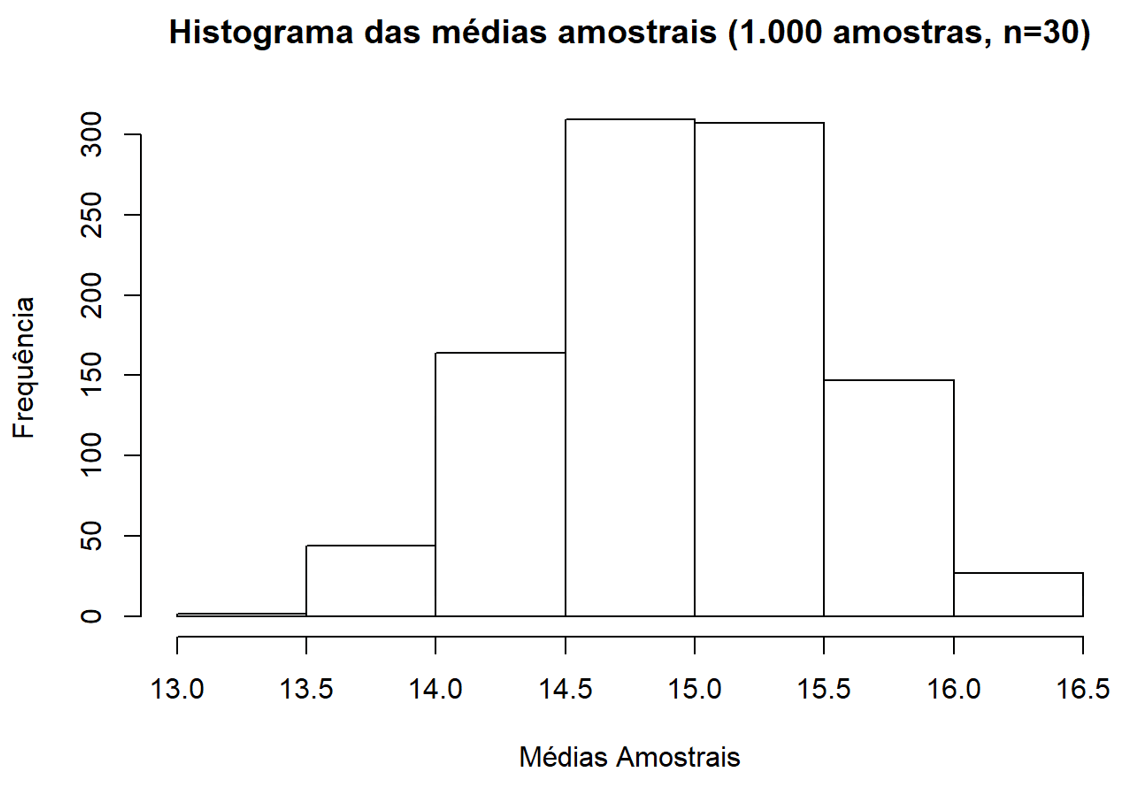
Notamos, portanto, que os valores gerados no primeiro histograma concentram-se em torno do valor 15, ao passo que a amostra inicial gerada (10.000 observações) tendia a uma distribuição normal, com média 15 e desvio padrão de 3. Da mesma forma, após criarmos as 1.000 com 30 observações e calcularmos suas respectivas médias, notamos que também existe uma convergência para 15. Se cada uma dessas amostras possuísse, ao invés de 30 observações, 200 elementos, notaríamos uma convergência ainda maior (perceba que o eixo x possui menor amplitude):
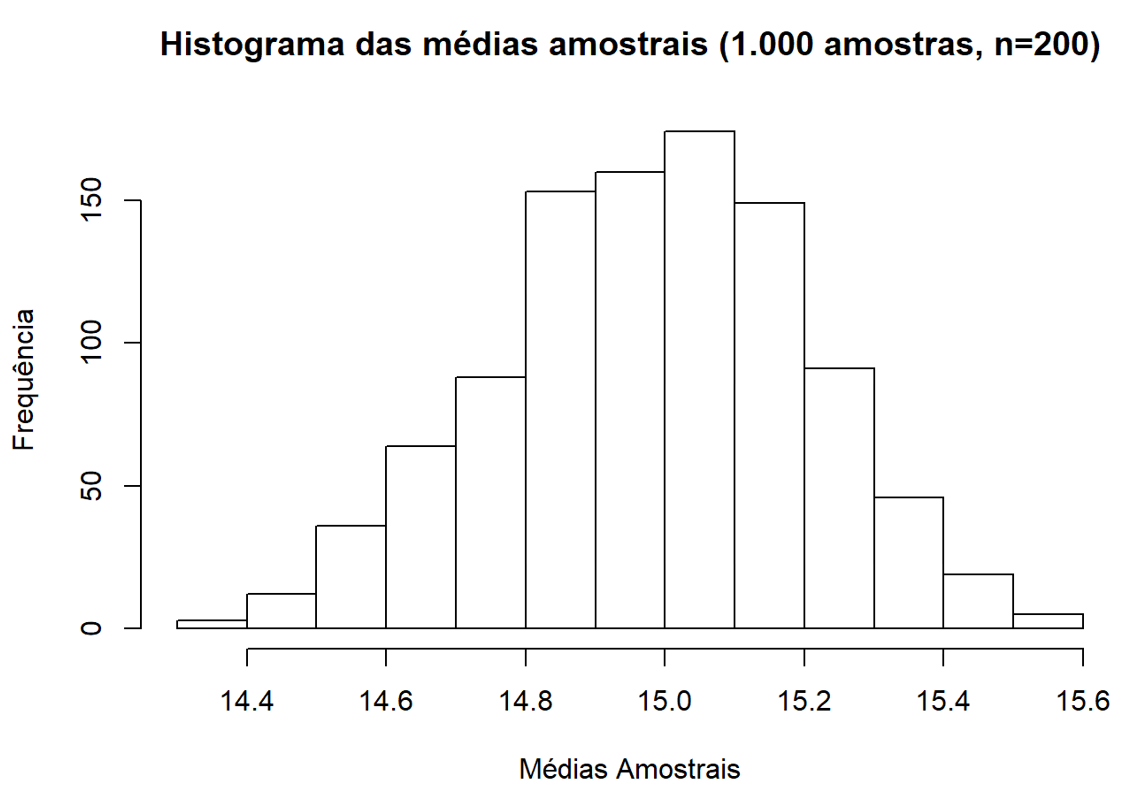
Verificamos, a partir de um exercício prático, o funcionamento do Teorema do Limite Central. No entanto, nossa amostra inicial gerada já era proveniente de uma distribuição normal, o que, em tese, facilitaria que as médias das amostras secundárias também tendessem à normalidade. Dessa forma, criamos um novo conjunto de dados, desta vez por meio de uma distribuição Binomial, expressamente discreta. Para tanto, foram geradas 10.000 observações de uma distribuição inominal com parâmetros n=20n=20 e p=0,03p=0,03:
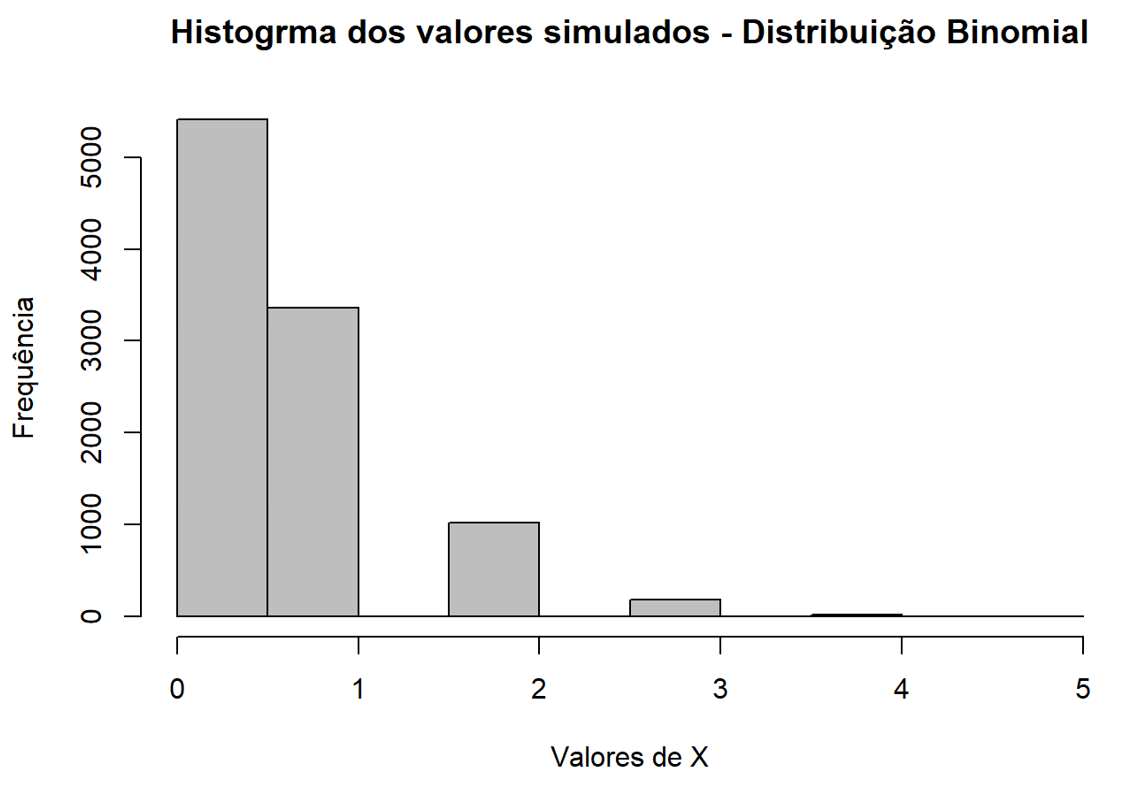
Gerando as amostras aleatórias:
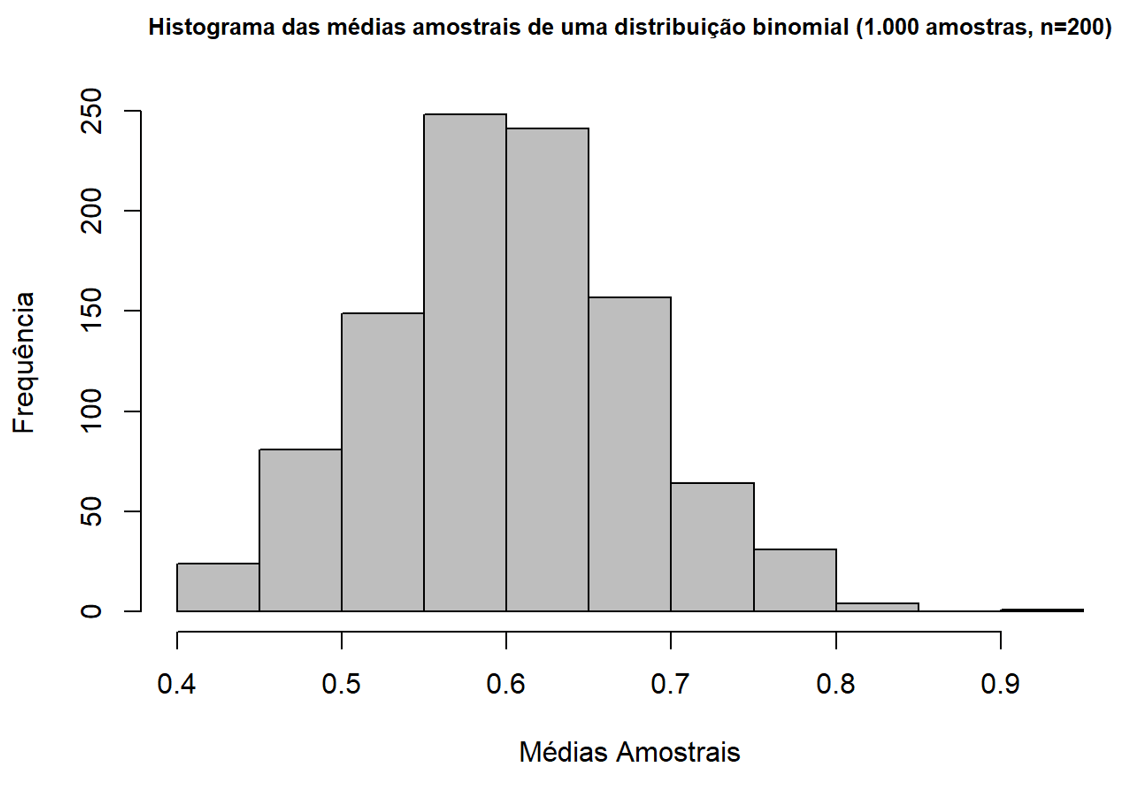
Nesse sentido, notamos que a média das amostras provenientes de uma distribuição binomial também tendem a um comportamento normal. Quando geramos a amostra inicial, com 100 observações, utilizamos como parâmetro de sucesso p=0,03p=0,03. O valor esperado E(X)=np=0,03×20=0,6E(X)=np=0,03×20=0,6. Notamos que as médias amostrais tendem a uma distribuição normal centralizada em 0,6, reforçando o Teorema do Limite Central.
Distribuições de Dados
Na segunda etapa de nossa atividade prática, trabalharemos com algumas diferentes distribuições, no intuito de compreendermos um pouco melhor seus parâmetros e seus respectivos impactos. Para tanto, utilizaremos duas distribuições discretas (Bernoulli e Poisson) e duas distribuições contínuas (Normal e Uniforme).
Distribuições Discretas
O R nos permite simular facilmente diversos tipos de distribuição, sejam elas discretas ou contínuas. Para simularmos valores aleatórios, utilizamos o comando r+nome da distribuição, o que nos abrirá a parametrização necessária para gerar o conjunto. Dessa forma, para trabalharmos com as distribuições Bernoulli e Poisson, utilizarmos os comandos rbern e rpois. Para o rbern, necessitamos instalar o pacote Rlab, enquanto o rpois já vem integrado ao RStudio.
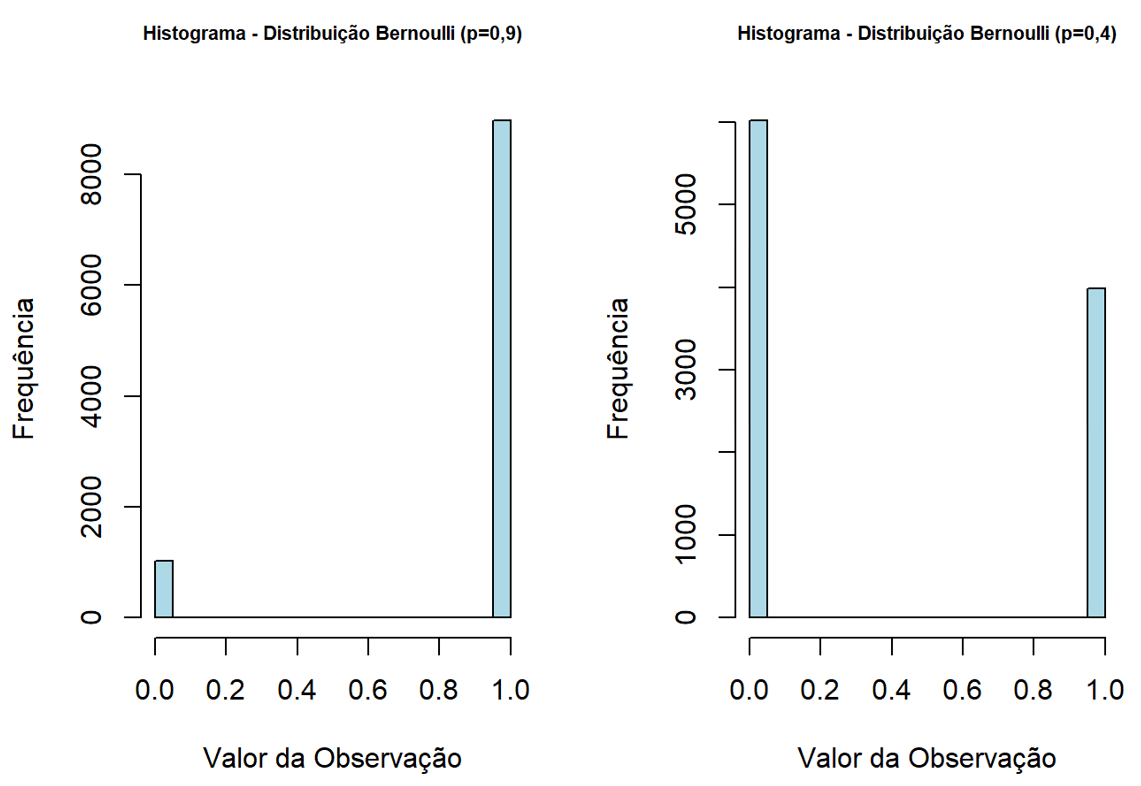
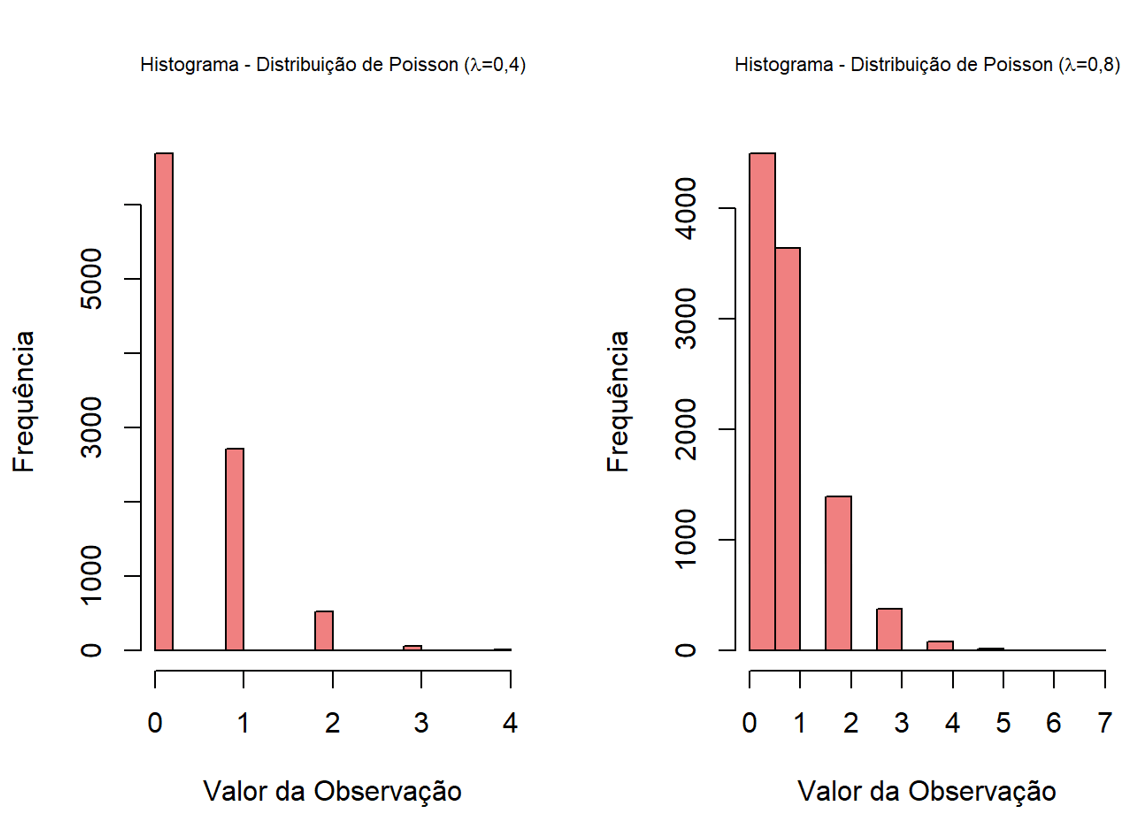
Para a distribuição de Poisson, temos o seguinte cenário:
Distribuições Contínuas
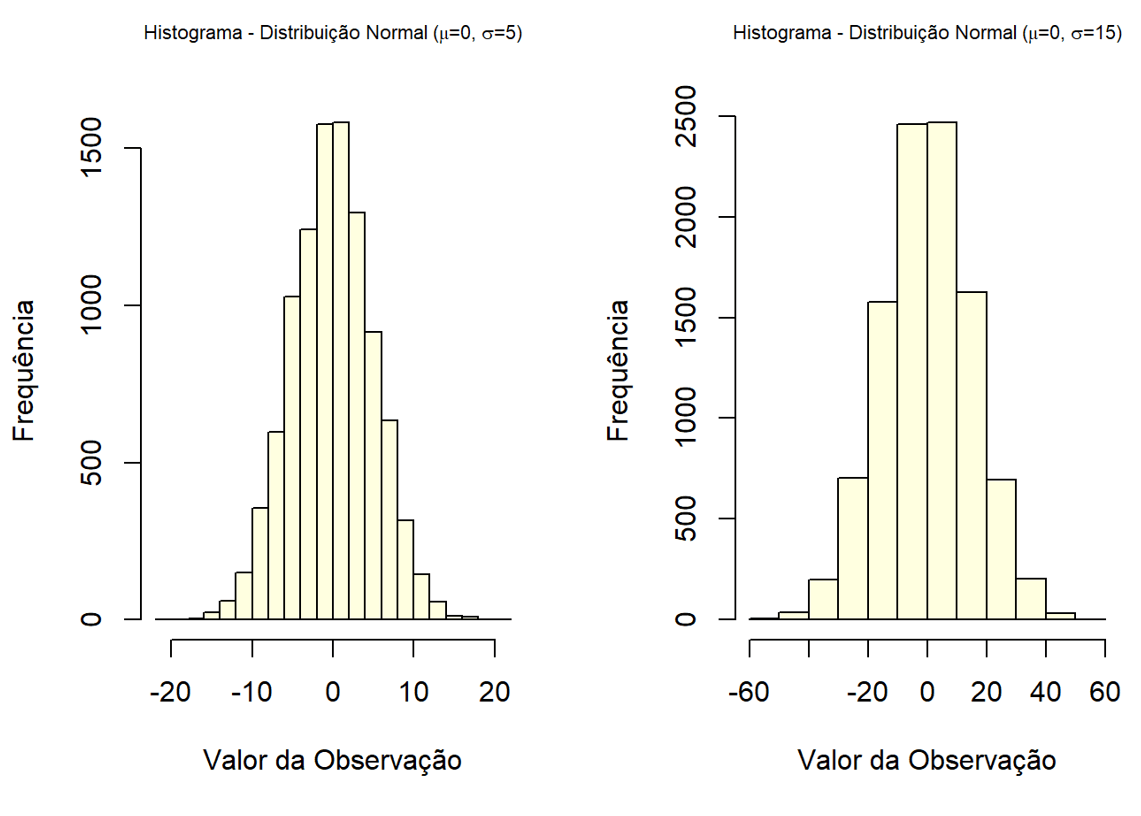
Para as distribuições contínuas, trabalharemos com dois casos específicos: a distribuição normal e a distribuição Uniforme. Para tanto, utilizaremos as funções rnorm e rpois para gerar os conjuntos e hist para gerar os gráficos:
Para a distribuição de Uniforme, temos o seguinte cenário:
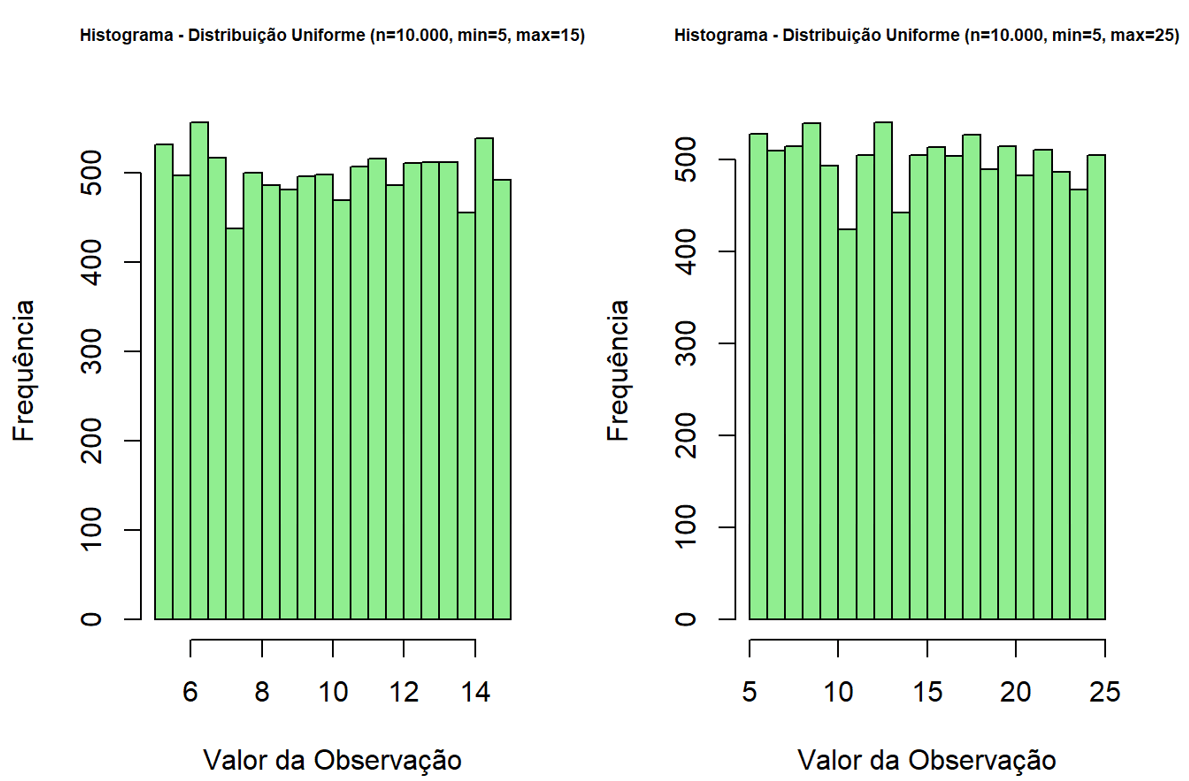
Observamos que a alteração dos limites da distribuição uniforme pouco altera seu formato. Nesse caso, a distribuição estaria mais suscetível ao tamanho amostral. Se alterarmos o valor de nn para 15, obteríamos o seguinte cenário:
Finalizamos o conteúdo prático desta seção, o que nos permitiu observar mais de perto o Teorema do Limite Central e conhecer um pouco melhor as distribuições de dados. Como sugestão para maior aprofundamento, é interessante realizar o mesmo processo que utilizamos no TLC, porém com outra distribuição qualquer.
Agora, faça você mesmo os testes utilizando o compilador que segue:
Para visualizar o objeto, acesse seu material digital.
Após cumprirmos o conteúdo prático desta seção, encerra-se a terceira unidade do livro. O conhecimento adquirido nas últimas três seções nos permite exercitar e trabalhar aspectos relacionados à amostragem, reamostragem e distribuição de dados, tanto para variáveis discretas quanto para variáveis contínuas. É mais um importante passo em sua formação em Probabilidade e Estatística para análise de dados. Novamente, parabéns por ter chegado até aqui. Vamos em frente, rumo à quarta e última unidade.
Faça valer a pena
Questão 1
Nível de confiança, margem de erro e intervalo de confiança são importantes conceitos da Estatística Inferencial. A esse respeito, complete as lacunas da sentença a seguir.
Margem de erro e nível de confiança são conceitos ______________. A(o) ________________ está associada(o) a um(a) __________________ que, de modo geral, assegura que a cada 100 repetições de um experimento, em 90 delas o parâmetro populacional estará inscrito dentro desta margem de erro, considerando um nível de confiança de _______________.
Assinale a alternativa que completa as lacunas corretamente.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Correto!
Margem de erro e nível de confiança são termos distintos. A margem de erro indica a possível variação entre um parâmetro amostral e um parâmetro populacional (geralmente desconhecido). À margem de erro, associa-se um nível de confiança, que garante que, a cada 100 repetições de um experimento, em x% deles o parâmetro populacional estará inscrito nessa margem. Para um nível de confiança de 90%, 90 a cada 100 experimentos apresentarão o resultado dentro dessa margem.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Questão 2
Cinco caminhões foram avaliados quanto ao desempenho de seus motores, no que diz respeito ao consumo de combustível. Os dados obtidos estão apresentados conforme a tabela a seguir:
| Caminhão | Rendimento (km/l) |
|---|---|
| 1 2 3 4 5 |
3,0 2,8 3,1 2,9 2,4 |
A partir do conjunto de dados inicial, foi realizada uma reamostragem, de onde se obteve um novo conjunto, com duas amostras bootstrap:
| Caminhão | Rendimento (km/l) | BP1 | BP2 |
|---|---|---|---|
| 1 2 3 4 5 |
3,0 2,8 3,1 2,9 2,4 |
2,9 2,8 2,4 2,8 2,8 |
2,8 3,0 2,4 2,9 3,0 |
Considerando o conjunto de dados apresentado, é correto afirmar que a média da amostra inicial e a média das amostras bootstrap equivalem, respectivamente, a:
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Correto!
A questão passa pela aplicação do cálculo dos parâmetros obtidos por meio de um processo de reamostragem. São solicitados dois valores médios: o primeiro da amostra inicial e o segundo relacionado às amostras bootstrap, tomadas em conjunto. Para o cálculo da média da amostra inicial, tem-se o seguinte processo:
.
Por outro lado, para calcularmos o valor médio das amostras bootstrap, devemos primeiro encontrar seus respectivos individuais e extrair a média desses valores:
.
Questão 3
O método de reamostragem Jackknife consiste na criação de amostras secundárias, que possuem, no mínimo, uma observação a menos do que a amostra original. Em uma análise realizada por uma consultoria, foi obtida uma amostra com cinco observações, distribuídas conforme a tabela a seguir:
| Observação | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Amostra Inicial | 15 | 14 | 15 | 13 | 12 |
A partir desse conjunto, foram criadas outras cinco amostras Jackknife, cada uma delas com um elemento a menos da amostra original, conforme apresentado a seguir:
| Observação | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Amostra Inicial | 15 | 14 | 15 | 13 | 12 |
| Jackknife 1 Jackknife 2 Jackknife 3 Jackknife 4 Jackknife 5 |
NA 15 15 15 15 |
14 NA 14 14 14 |
15 15 NA 15 15 |
13 13 13 NA 13 |
12 12 12 12 NA |
Considerando os dados apresentados, a diferença entre a média dos desvios padrão das amostras Jackknife e o desvio padrão da amostra inicial é de:
Correto!
A questão passa pela aplicação dos conceitos relacionados à reamostragem pelo método Jackknife. É solicitado o valor da diferença entre a média dos desvios padrão das amostras Jackknife e o desvio padrão da amostra inicial. Para tanto, devemos calcular os seguintes valores:
| Observação | 1 | 2 | 3 | 4 | 5 | Média | n-1 | Desvio Padrão | |
|---|---|---|---|---|---|---|---|---|---|
| Amostra Inicial | 15 | 14 | 15 | 13 | 12 | 13,8 | 6,8 | 4 | 1,30 |
| Jackknife 1 Jackknife 2 Jackknife 3 Jackknife 4 Jackknife 5 |
NA 15 15 15 15 |
14 NA 14 14 14 |
15 15 NA 15 15 |
13 13 13 NA 13 |
12 12 12 12 NA |
13,5 13,75 13,5 14 14,25 |
5 6,75 5,00 6,00 2,75 |
3 3 3 3 3 |
1,29 1,50 1,29 1,41 0,96 |
Nesse sentido, o desvio padrão da amostra inicial é de 1,30. Por outro lado, ainda é necessário calcular a média dos desvios das amostras Jackknife, dada por . A diferença entre as médias, portanto, é de 1,29-1,30=-0,01.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Referências
RIZZO, A. L. T.; CYMROT, R. Utilização da técnica de reamostragem bootstrap em aplicação na Engenharia de Produção. Anais: X Encontro Latino-Americano de Iniciação Científica e VI Encontro Latino-Americano de Pós-graduação, Universidade do Vale, São Paulo, p. 488, 2006.
SILVA, G. F. S. Fraude de cartão de crédito: como a estatística e o machine learning se conversam. Dissertação de Mestrado. Estatística e Experimentação Agronômica. Esalq - Universidade de São Paulo, Piracicaba, 2020.












