lorem ipsum dolor sit amet
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nunc dignissim euismod urna tincidunt sagittis. Vivamus id vehicula eros, non scelerisque eros.

Fonte: Shutterstock.
Praticar para aprender
Caro aluno
Nesta seção, abordaremos uma série de conteúdos importantes para a análise de dados. Apesar de um pouco densos, os tópicos apresentados nos darão base para explorar análises de grande relevância na Estatística e Probabilidade, como Teste de Médias, Teste de Hipóteses, Teste Qui-quadrado, entre outros assuntos que trabalharemos nas próximas seções.
A questão central com que trabalharemos é a diferenciação de distribuições advindas de variáveis aleatórias contínuas e discretas. Na segunda seção da Unidade 1, discutimos os tipos de variáveis, como quantitativa e qualitativa, além das variáveis e discretas. Para refrescar a memória, iniciaremos o texto retomando brevemente o assunto.
Em seguida, entraremos nos tópicos de distribuição de dados e probabilidade, que nos permitirá explorar três conceitos distintos: a função de probabilidade, a função de distribuição acumulada e a função de densidade de probabilidade.
Após isso, entraremos nas modelagens das distribuições de variáveis aleatórias, mas não se assuste com as fórmulas! Não é necessário decorá-las, ao passo que, em situações reais, temos o auxílio dos softwares estatísticos e das linguagens de programação. Atente-se aos principais comportamentos das distribuições, em termos de estrutura de parâmetros e forma das curvas por meio da análise gráfica. Trataremos, nesta parte, das distribuições de Bernoulli, Binomial, Poisson, Geométrica e Hipergeométrica.
Compreendidas as distribuições de variáveis discretas, trataremos das contínuas, representadas pela Uniforme, Exponencial, Gama, Beta, Normal, Z, t de Student, F de Fisher-Snedecor e Qui-quadrado. Novamente, não é necessário decorar todas as estruturas de função de densidade de probabilidade, mas é de grande importância compreender as diferenças entre as distribuições.
Esta é uma seção um pouco mais teórica do que as demais, mas é de grande importância construirmos um conhecimento sólido para melhor explorarmos os próximos assuntos. Trabalhe todos os recursos disponíveis, como material complementar, os boxes de Assimile, Reflita e Exemplificando, bem como os exercícios da seção, pois certamente colaborarão para o melhor entendimento dos assuntos abordados.
Caro aluno, a atividade de análise de dados apresenta diversos desafios em seu dia a dia, o que a faz ainda mais interessante. Frequentemente, deparamo-nos com situações que nos tiram de uma zona de conforto e nos fazem buscar formas de resolver problemas. Algo comum, por exemplo, é a limitação operacional em situações que envolvem populações com um grande número de observações. Como proceder uma análise de dados de uma empresa com 20.000, 30.000 ou até 100.000 funcionários? Ou, então, como realizar uma pesquisa eleitoral que indique as intenções de votos dos habitantes de um país? É preciso entrevistar cada um deles para que se obtenha um número representativo? A resposta é não! E é nesse sentido que se encaixa importante conceito na análise de dados, a amostragem.
Outro tópico de grande relevância na análise de dados é análise de distribuição. O que faz, por exemplo, um conjunto de dados possuir um comportamento semelhante a um sino, na denominada distribuição normal? Ou em que contexto utilizamos uma distribuição t de Student? A compreensão destes conceitos é fundamental para que se avance em análises ainda mais interessantes, como o cálculo dos intervalos de confiança, a comparação estatística de médias, entre outras. Portanto, dominar tanto o processo de amostragem quanto a análise de distribuição é de suma importância para a resolução de problemas práticos da atividade de análise de dados.
Você é especialista em dados de uma empresa e está realizando um workshop sobre distribuição de dados, como forma de apresentar aos colaboradores uma visão simplificada e de fácil entendimento. Para tanto, você deverá realizar algumas simulações no R e plotar gráficos comparativos de quatro distribuições específicas: normal, exponencial, uniforme e binomial. Deixe claro os parâmetros utilizados e as diferenças entre o comportamento das distribuições.
conceito-chave
Na Estatística e Probabilidade, muito se trabalha com o conceito de variável aleatória. Para compreendermos este ponto, é necessário resgatar alguns temas, como espaço amostral e evento. De modo geral, a relação entre esses termos é dada da seguinte maneira: o espaço amostral refere-se a todos os eventos possíveis de um fenômeno aleatório, ou seja, todos os valores que um evento pode assumir. Nesse sentido, uma variável aleatória é aquela cujos valores são oriundos de um experimento aleatório e que estão dentro de um espaço amostral (YALE, 1997).
As variáveis aleatórias distinguem-se em dois tipos: discretas e contínuas. Essa classificação está associada aos próprios conceitos de variáveis discretas e contínuas que vimos na primeira unidade deste livro.
Nesse sentido, uma variável aleatória discreta é aquela que assume um conjunto finito de valores. Suponha, por exemplo, que uma variável qualquer possui um conjunto finito de valores, dados por , com . A cada elemento associa-se uma probabilidade , de modo a ser criada uma relação, conforme a Tabela 3.3.
O termo é designado por função de probabilidade e expressa, de forma geral, cada valor de um conjunto de dados a uma probabilidade, que pode ser a mesma para todos, caracterizando eventos equiprováveis, ou distintas. Dessa forma, com base na função de probabilidade, tem-se as seguintes pressuposições:
Exemplificando
No lançamento simultâneo de duas moedas, temos quatro possíveis resultados: (CARA, CARA); (CARA, COROA); (COROA, CARA); (COROA, COROA). Dessa forma, a função de probabilidade é dada por:
| Resultado (x) | |
|---|---|
| (CARA, CARA) (CARA, COROA) (COROA, CARA) (COROA, COROA) |
|
| Total | 1 |
A probabilidade, portanto, de as duas moedas apresentaram faces distintas é dada por: . De modo análogo, a probabilidade de as duas moedas apresentarem a mesma face é expressa por: . O somatório das probabilidades equivale a 1, corroborando a segunda proposição apresentada anteriormente. Além disso, todas as probabilidades estão dentro de um intervalo , contemplando a terceira proposição.
A partir da função de probabilidade, podemos introduzir outro conceito: a função de distribuição acumulada (f.d.a.), representa por . Na linha do mesmo exemplo construído, a f.d.a. é dada pela probabilidade de assumir um valor menor ou igual a , ou seja, .
Suponha, por exemplo, que uma variável tenha a função de probabilidade, conforme expresso na Tabela 3.4:
| 5 7 9 10 |
0,20 0,35 0,30 0,15 |
| Total | 1,00 |
Nesse sentido, a maior probabilidade de ocorrência está associada ao número 7, com 35%, seguido por 9 (30%), 5 (20%) e 10 (15%). Assim, podemos realizar algumas considerações a respeito do conjunto de dados:
- A probabilidade de um evento ser menor do que 5 é equivalente a 0, ao passo que 5 é o valor mínimo do conjunto. Assim, . No entanto, a probabilidade de ser menor ou igual a 5 deve incluir a probabilidade associada ao valor 5, ou seja, .
- A probabilidade de X assumir valor igual a 7 é equivalente a 0,35. No entanto, a probabilidade de X ser menor ou igual a 7 é dada por: . Dessa forma, tem-se que .
- De modo análogo, a probabilidade de X assumir um valor menor igual a 9 é equivalente à probabilidade associada ao número 9 somada à probabilidade dos elementos anteriores, ou seja, . Assim, .
- Por fim, como o valor máximo possível do conjunto de dados é 10, tem-se que , de modo que .
| 5 7 9 10 |
0,20 0,35 0,30 0,15 |
0,20 0,55 0,85 1,00 |
| Total | 1,00 |
Fica claro, portanto, a diferença entre a função de probabilidade e a função de distribuição acumulada . Graficamente, a Figura 3.6 permite identificar a distinção entre os dois conceitos.

A função de distribuição acumulada aplica-se ao caso de variáveis aleatórias discretas que, como vimos, assumem um conjunto finito de dados e provém, na maior parte, de processos de contagem. No exemplo realizado, os dados poderiam ser provenientes da idade dos filhos dos colaboradores de uma empresa, total de peças defeituosas que uma fábrica produz por dia, número de pessoas vacinadas em uma unidade de saúde, entre outras possibilidades. Assim como as variáveis discretas, também é possível trabalhar com a função de distribuição acumulada. Entretanto, é mais comum utilizarmos outra ferramenta: a função de densidade de probabilidade, representada por , porque as variáveis aleatórias contínuas não assumem valores exatos e finitos.
reflita
Comumente, as variáveis aleatórias contínuas são provenientes de processos de mensuração, como a aferição da pressão arterial ou, simplesmente, a obtenção da altura de duas pessoas. Mas, se pararmos para refletir, a altura de um indivíduo é uma medida exata? E a resposta é não. Quando medimos alguém ou a nós mesmos, o valor obtido refere-se a uma aproximação da nossa altura “verdadeira” porque, quando uma pessoa cuja altura apresentada na fita métrica é de 1,80 metros, ela mede, na verdade, um valor próximo a isso, como 1,800135...m ou 1,800458...m. Dessa forma, por mais que o valor arredondado seja o mesmo, dificilmente encontraremos duas pessoas com alturas exatamente iguais. O mesmo pensamento se aplica para praticamente todos os processos de mensuração.
Nesse sentido, em casos de variáveis contínuas, buscamos a probabilidade de X assumir um valor dentro de um intervalo definido , ou seja, . Dessa forma, suponha a função de densidade de probabilidade , representada na Figura 3.7.

Nessa função de densidade de probabilidade, estamos avaliando a probabilidade de X assumir um valor entre -1 e 1, ou seja, , que equivale à área do polígono destacado em azul. Se esse polígono fosse um retângulo, por exemplo, facilmente encontraríamos a probabilidade associada aos valores. No entanto, devido à não regularidade da forma, é necessário aplicar o cálculo da integral da função definida para encontrarmos a respectiva área. Não entraremos nesse conteúdo com profundidade. Aqui, é suficiente compreendermos que:
- (lê-se: a função de densidade de probabilidade assume valores maiores ou igual a zero para todo xis pertencente ao conjunto dos números reais).
- (lê-se: a integral definida de f(x) no intervalo de a é igual a um. O conceito é equivalente à propriedade da função de distribuição acumulada, em que ).
Para demonstração, daremos um exemplo de cálculo da probabilidade com base em uma função de distribuição de probabilidade. Suponha que X seja uma variável aleatória contínua, com função de distribuição de probabilidade dada por , com . A probabilidade de estar entre 0,4 e 0,6 é obtida através dos seguintes cálculos:
Nesse sentido, a probabilidade de estar entre 0,4 e 0,6 é de aproximadamente 15,20%.
Reflita
Como falamos anteriormente, ao trabalharmos com variáveis aleatórias contínuas, é praticamente impossível obter dois valores exatamente iguais. Isso porque as casas decimais, quando abertas, embora possam estar próximas, serão distintas conforme se aumenta o número de casas. Por essa razão, não é comum encontrarmos cálculos de probabilidade de variáveis aleatórias contínuas que envolvem a probabilidade exata de um intervalo acontecer. Geralmente, trabalhamos com valores intervalados, ou seja, com a chance de determinada observação ser menor ou igual, estar entre, ou ser maior ou igual a um intervalo específico da distribuição.
Compreendidos os conceitos de função de distribuição acumulada (f.d.a.) e função de densidade de probabilidade (f.d.p.), temos elementos suficientes para compreender um pouco melhor a respeito das distribuições de dados. De modo geral, existem diversos tipos de distribuição de dados, divididas em dois grandes grupos: discretas e contínuas. Para as variáveis aleatórias discretas, temos os casos das distribuições de Bernoulli, Binomial, Hipergeométrica, Poisson e Geométrica (BUSSAB; MORETTIN, 2010). Por outro lado, para as variáveis aleatórias contínuas, destacam-se as distribuições Uniforme, Normal, Exponencial, Gama, Beta, Qui-quadrado, t de Student e F de Fisher-Snedecor. Existem outras distribuições associadas aos respectivos grupos, mas essas costumam ser as principais.
A Figura 3.8 apresenta alguns exemplos de distribuições de variáveis discretas, considerando cinco tipos diferentes. A distribuição de Bernoulli, por exemplo, claramente possui somente dois valores possíveis. A Binomial, por outro lado, pode ter mais. Os gráficos foram simulados com parâmetros distintos. Se alterarmos os parâmetros, como tamanho amostral, probabilidade de sucesso, entre outros, podemos ter novos formatos dentro das distribuições apresentadas. A depender dos parâmetros, por exemplo, a distribuição geométrica, que se demonstrou bastante assimétrica para os valores simulados, pode apresentar uma suavização maior. Hipergeométrica, por outro lado, pode parecer cada vez mais com uma distribuição Normal. Os formatos, portanto, não são exatamente fixos.

Além do formato, as distribuições de variáveis aleatórias discretas também são distintas em relação às funções de distribuição acumulada e aos parâmetros por elas incorporados. O Quadro 3.2, adaptado de Bussab e Morettin (2010), apresenta as principais características das distribuições de variáveis aleatórias discretas. O quadro apresenta uma coluna com duas propriedades importantes: o valor esperado que, de modo geral, refere-se à expectativa do valor da média populacional, e a variância de X.
| Distribuição | Parâmetros | ||
|---|---|---|---|
| Bernoulli | • p: probabilidade de sucesso do evento. | ||
| Binomial | • n: número total de observações (amostra); • p: probabilidade de sucesso do evento. |
||
| Poisson | • k: número de sucessos; • n: número total de observações (amostra); • |
||
| Hipergeométrica | • N: tamanho populacional; • n: número total de observações (amostra); • r: instâncias classificadas com determinada característica A. • N-r: instâncias classificadas sem a característica A. |
||
| Geométrica | • p: probabilidade de sucesso do evento. |
No caso das distribuições de variáveis aleatórias contínuas, a ideia é semelhante. Cada uma das distribuições possui uma função de densidade de probabilidade diferente, que afeta diretamente suas respectivas curvas. Além da f.d.p., outro fator de impacto são os valores atribuídos aos parâmetros. A Figura 3.9 apresenta alguns exemplos de distribuições de variáveis aleatórias contínuas.

Em princípio, se comparamos somente o formato das distribuições, podemos retirar alguma informação errônea. A distribuição de Poisson presente na Figura 3.8 e a distribuição Exponencial da Figura 3.9, por exemplo, possuem formatos muito semelhantes, o que nos poderia levar a tomar alguma decisão precipitada. Há de se lembrar, no entanto, que uma trabalha com valores discretos e outra com contínuos são distribuições distintas já no tipo de variável. Em termos dos parâmetros e das funções de densidade de probabilidade, as distribuições de variável aleatória contínua diferenciam-se conforme sintetizado no Quadro 3.3.
| Distribuição | Parâmetros | ||
|---|---|---|---|
| Uniforme | • : limite mínimo do intervalo de dados; • : limite máximo do intervalo de dados. |
||
| Exponencial | • : indica a taxa de ocorrência por unidade de medida (MAGALHÃES, 2015).; |
||
| Beta | • e : são parâmetros que definem a forma e a escala da distribuição. |
||
| Gama | • e : são parâmetros positivos (MAGALHÃES, 2015); • é a função Gama. |
||
| Normal | • : desvio padrão populacional; • : Média populacional. |
Apesar das diversas distribuições apresentadas, tanto advindas de variáveis aleatórias discretas quanto de contínuas, daremos foco na distribuição normal que, além de compor diversos modelos de análise estatística, é a raiz para os desdobramentos de outras distribuições, como a Z e a t de Student.
Como vimos, a função de densidade de probabilidade de uma distribuição normal é dada por:
É essa função, portanto, que nos dará uma distribuição com aquele formato de sino característico. Além do formato, a curva respectiva da função de densidade de probabilidade nos permite obter a probabilidade de um valor estar inserido em um intervalo específico. Para tanto, é comum utilizarmos o cálculo integral definido para obter as probabilidades de distribuições contínuas. Quando falamos da distribuição normal, no entanto, existe uma propriedade que nos permite obter o valor das probabilidades com base nas médias e nos desvios populacionais. Tal propriedade é expressa na Tabela 3.6.
| Intervalo | Proporção das observações contempladas (probabilidade) | ||
|---|---|---|---|
| 68,26% 95,44% 99,73% |
|||
Nesse sentido, quando trabalhamos com a média populacional acrescida de um desvio acima e um desvio abaixo, contemplamos 68,26% das observações. De modo similar, quando diante da média acrescida de dois desvios para cima e dois para baixo, o valor sobe para 95,44%. Para três desvios, 99,73% das observações são contempladas. A Figura 3.10 ajuda-nos a melhor interpretar esse comportamento. Observe as faixas de concentração para , e , e o percentual dos dados que cada uma contempla.
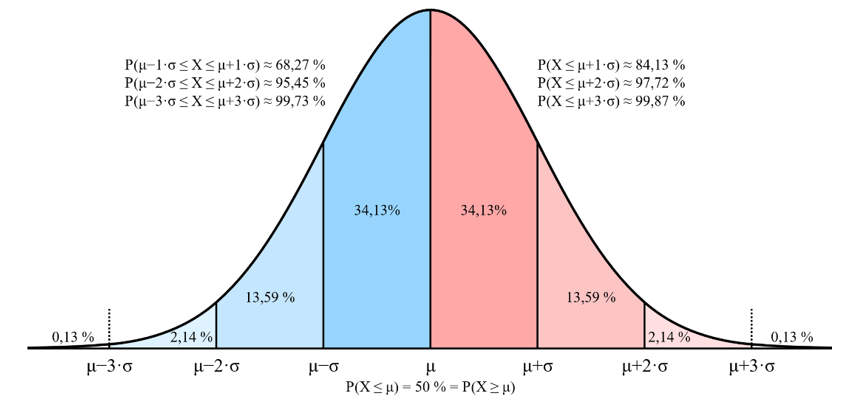
No entanto, por mais que esse comportamento nos ajude a calcular as probabilidades nesses pontos gerais, na prática, dificilmente trabalharemos com esse tipo de situação, ou seja, desejaremos calcular as probabilidades relativas a áreas específicas. Nesse contexto se insere a distribuição Z, também denominada normal padrão. Suponha que X seja uma variável aleatória tal que . Nesse caso, a média populacional e a variância populacional podem assumir quaisquer valores, que dependerão das características das observações. Por outro lado, quando trabalhamos com a distribuição Z, os parâmetros de média e variância são sempre, respectivamente, 0 e 1, ou seja, . Dessa forma, estamos padronizando os parâmetros da distribuição para valores fixos. Basicamente, o que fazemos é uma redução de uma distribuição para uma distribuição . Para tanto, é utilizada a seguinte fórmula:
Suponha, portanto, que estamos trabalhando com uma distribuição normal com média equivalente a 10 e desvio padrão de 7,5. Desejamos, portanto, encontrar o valor de equivalente em . Para tanto, temos que:
Na última seção deste livro, trabalharemos algumas aplicações da distribuição Z. Por ora, é importante sabermos suas principais características e conseguirmos encontrar o respectivo valor de X em Z.
Além da distribuição Z, outra importante distribuição é a t de Student, cuja função de densidade de probabilidade é dada por:
Em que é o número de graus de liberdade.
Assimile
Ao trabalharmos com análises estatísticas, é muito comum nos depararmos com o conceito de graus de liberdade. Basicamente, a ideia é obter um número de observações que estejam livres para variar de acordo com uma regra de restrição específica. Por exemplo: suponha que um professor esteja avaliando um trabalho de quatro alunos. A nota do trabalho será atribuída de 0 a 40 para o grupo, ficando a critério dos alunos a alocação entre os quatro membros. Um dos grupos obteve nota 35. O primeiro aluno teve a liberdade de escolha, atribuindo um valor de 10 por considerar ter feito a maior parte do trabalho. Outros dois alunos, que também participaram bastante da elaboração, também escolheram suas notas, ambas no valor de 9. Somando as três notas, temos um total de 28. Assim, cabe ao último aluno somente a nota 7, que é o valor que falta para os 35 atribuídos pelo professor. Nesse sentido, podemos observar que somente três dos quatro alunos tiveram a liberdade de escolher suas notas, cabendo ao quarto aluno completar o valor para atingir a nota geral de 35.
Apesar do exemplo ilustrativo, na prática, a ideia é semelhante. Suponha que estamos diante de uma amostra com n observações e desejamos calcular a média amostral. Para tanto, na obtenção dessa estimativa, temos n-1 graus de liberdade. Se desejássemos, por exemplo, calcular alguma outra estimativa, gastaríamos mais um grau de liberdade, ou seja, para uma situação que envolva o cálculo de p parâmetros, teremos n-p graus de liberdade.
Assim como a distribuição Z, a t de Student tende à normalidade, com média centrada em 0. A variância, no entanto, é dada por , ou seja, . Conforme apresentado pela Figura 3.11, para valores de v elevados, a distribuição t passa a ter variância com tendência a 1, ou seja, mesmo valor da distribuição Z.

Tanto a distribuição Z, quando a t de Student são utilizadas para testes estatísticos de comparação entre médias, assunto que veremos mais adiante. No geral, para amostras com , utilizamos a estatística t para o teste de médias. No entanto, quando , trabalha-se com a estatística Z.
Além dessas duas distribuições citadas, é comum trabalharmos com algumas outras distribuições específicas, como a F de Fisher-Snedecor e a Qui-quadrado, que também possuem valores de probabilidade tabelados, facilitando os cálculos relacionados a essas duas distribuições. A distribuição F é utilizada na Análise de Variância em que se comparam duas ou mais médias de grupos distintos. Por outro lado, a distribuição Qui-quadrado é constantemente aplicada no teste Qui-Quadrado para comparação de variáveis categóricas.
Embora os formatos se assemelhem, as distribuições F e Qui-quadrado são bastante distintas quanto à função densidade de probabilidade. A f.d.p. para a distribuição F é dada por:
Por outro lado, a Qui-quadrado possui a seguinte função de densidade:
Apesar da maior parte dessas distribuições parecerem de grande complexidade, ao trabalharmos na prática precisaremos conhecer a ideia por trás delas, não sendo necessário memorizar todas as funções de probabilidade, ao passo que temos o auxílio de diversas ferramentas de cálculo, como o R. A partir das próximas seções, as diferenças entre as distribuições ficarão cada vez mais claras, ao passo que exercitaremos questões práticas de aplicação, como os testes de médias e intervalos de confiança.
Parabéns por ter chegado até aqui! Continue seus estudos e siga em frente!
Faça valer a pena
Questão 1
No lançamento de um dado, existem seis possíveis resultados, apresentados na tabela abaixo:
| Resultado (x) | |
|---|---|
| 1 2 3 4 5 6 |
|
| Total | 1 |
Considerando a tabela apresentada, assinale a alternativa que apresenta corretamente a probabilidade de se obter um lançamento com um resultado par.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Correto!
A questão passa pela aplicação do cálculo de probabilidade com base em uma função de probabilidade. Dentre os seis eventos possíveis, três deles apresentam valores pares: (2, 4 e 6). Dessa forma, a probabilidade desejada é dada por .
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Questão 2
Uma empresa está realizando uma análise de perfil de seus funcionários, considerando as seguintes variáveis: peso, altura, número de filhos, número de efetivações e tempo de deslocamento até o trabalho.
Com base nas cinco variáveis analisadas pela empresa, assinale a alternativa que apresenta somente variáveis discretas.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Correto!
A questão aborda a aplicação do conhecimento relacionado aos tipos de variáveis, expressamente discretas e contínuas. Dentre as variáveis apresentadas, tem-se a seguinte relação:
• Peso: variável contínua, obtida através de um processo de mensuração e apresentada, geralmente, em kg.
• Altura: variável contínua, obtida através de um processo de mensuração e apresentada, geralmente, em metros.
• Número de filhos: variável discreta, ao passo que representa uma contagem finita.
• Número de efetivações: variável discreta, ao passo que representa uma contagem finita.
• Tempo de deslocamento até o trabalho: obtido através de um processo de mensuração e apresentada, geralmente, em horas ou minutos.
Nesse sentido, as únicas variáveis discretas da análise são número de filhos e número de efetivações.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Questão 3
Os retornos (r) de um investimento A possuem uma distribuição normal, tal que . Sabe-se que, em uma distribuição normal, a concentração das observações é dada a partir da relação a seguir:
| Intervalo | Proporção das observações contempladas (probabilidade) |
|---|---|
| 68,26% 95,44% 99,73% |
|
Considerando as informações apresentadas, é correto afirmar que o intervalo [-3%, 3%] engloba:
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Correto!
A questão passa pela aplicação da distribuição normal, especificamente o cálculo das proporções englobadas pelos intervalos baseados na média e no desvio padrão. O intervalo apresentado refere-se àquele em que os limites equivalem a . Como e , tem-se que . Como representa 68,26% de uma distribuição normal, a alternativa correta é: 68,26% das observações.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Referências
ALTMAN, D. G.; BLAND, J. M. Statistics notes: the normal distribution. Bmj, v. 310, n. 6975, p. 298, 1995.
BUSSAB, W. de O.; MORETTIN, P. A. Estatística básica. In: Estatística básica. p. xvi, 540-xvi, 540, 2010
YALE. Random Variables. Disponível em: https://bit.ly/3xUcFIN. Acesso em: 26 mar. 2021.



