Fonte: Shutterstock.
Deseja ouvir este material?
Áudio disponível no material digital.
praticar para aprender
Prezado estudante, nesta seção trabalharemos com as medidas de dispersão, importantes ferramentas no contexto de análise de dados. Tais medidas estão associadas ao termo variação. Quando trabalhamos com rendimentos variáveis, por exemplo, quanto maior a variação, maior o risco associado àquele ativo, podendo, dessa forma, obter-se um alto retorno, bem como um alto prejuízo, devido ao risco associado a ele.
Compreender a usabilidade dessas ferramentas é fundamental para a compreensão e análise de dados. Por essa razão, iniciaremos a seção com uma introdução às medidas de dispersão, destacando as duas principais funcionalidades.
Em seguida, trataremos do conceito de amplitude, passando por desvio médio absoluto, variância, desvio padrão e covariância.
Da mesma maneira que na seção anterior, buscamos apresentar um conteúdo de abordagem prática, com a utilização da linguagem R e do software RStudio.
Ao final da seção, você encontrará, como de costume, alguns exercícios de fixação. Não deixe de realizá-los, pois certamente colaborarão para um melhor aprendizado ao longo dessa trajetória.
Na situação-problema, encontraremos uma circunstância desafiadora, que serve para enriquecer nossos conhecimentos.
Considerando que se trata de um conteúdo com grande relevância, recomendamos a exploração de todos os recursos de aprendizagem disponíveis, como os scripts em R, a segunda situação-problema, bem como a leitura do material complementar.
O domínio das ferramentas de Estatística e Probabilidade é fundamental para o exercício da profissão de análise de dados, mesmo que se trabalhe de forma direta ou indireta com a geração de informações. Uma das mais importantes etapas de uma análise é a análise inicial, também denominada exploratória, em que conhecemos um pouco mais a respeito do conjunto de dados com que estamos trabalhando. Nesse sentido, destacam-se as medidas de localização, as medidas de dispersão e outras ferramentas como as separatrizes, e as representações gráficas, como o boxplot. O domínio de suas aplicações e a escolha correta das ferramentas que melhor apresentem a informação a ser transmitida são de grande relevância para situações e problemas práticos.
Você é analista de dados e está trabalhando em conjunto com a área de metrologia e qualidade de uma empresa do setor agrícola. Vocês estão realizando a seleção de fornecedores de um reagente utilizado na produção de defensivos naturais. Para tanto, vocês coletaram duas variáveis: preço por litro do reagente e rendimento do produto por hectare (ex.: 3 litros/hectare). A variável de interesse analisada será o custo por hectare de cada um dos produtos, conforme disposto na Tabela 2.5.
Tabela 2.5 | Dados referentes ao preço e rendimento de aplicação dos produtos por hectare
Fonte: elaborada pelo autor.
| Produto | Preço/litro | Rendimento (L/ha) | Custo/ha |
|---|---|---|---|
| 1 | R$ 51,00 | 4,93 | R$ 251,43 |
| 2 | R$ 56,00 | 5,69 | R$ 318,64 |
| 3 | R$ 90,00 | 3,07 | R$ 276,30 |
| 4 | R$ 150,00 | 6,21 | R$ 931,50 |
| 5 | R$ 109,00 | 8,6 | R$ 937,40 |
| 6 | R$ 165,00 | 3,38 | R$ 557,70 |
| 7 | R$ 25,00 | 8,6 | R$ 215,00 |
| 8 | R$ 39,00 | 5,45 | R$ 212,55 |
| 9 | R$ 58,00 | 12,44 | R$ 721,52 |
| 10 | R$ 70,00 | 6,77 | R$ 473,90 |
| 11 | R$ 44,00 | 6,98 | R$ 307,12 |
| 12 | R$ 48,00 | 5,19 | R$ 249,12 |
| 13 | R$ 75,00 | 4,95 | R$ 371,25 |
| 14 | R$ 55,00 | 3,65 | R$ 200,75 |
| 15 | R$ 78,00 | 4,35 | R$ 339,30 |
Para a seleção dos reagentes passíveis de utilização, considerando que todos trazem o mínimo de impacto ambiental possível, você e a equipe elaboraram um gráfico de controle, de modo que os produtos que ficaram fora dos limites sejam retirados do escopo de utilização da empresa. Existem dois limites de controle: o superior (LS) e o inferior (LI). O cálculo é dado por:
Ainda trabalharemos esse conteúdo com maior profundidade nas próximas unidades, mas, em uma distribuição normal – aquela caracterizada por um formato de sino –, quando consideramos 2 desvios acima e 2 desvios abaixo de sua média, contemplamos 95,45% das observações. Quando alteramos esse valor para 3 desvios , 99,73% das observações são englobadas. Considerando as fórmulas para cálculo dos limites, você deverá realizar duas simulações: a primeira, considerando e a segunda . Quais observações ficaram fora dos limites quando ? E quais ficaram para ?
Uma excelente aula!
conceito-chave
A atividade de análise de dados traz consigo uma série de ferramentas necessárias para o bom exercício da profissão. Entre elas, no contexto da análise exploratória, estão as medidas de dispersão, notadamente representadas pela amplitude, desvio padrão, variância e covariância. No dia a dia, tais medidas não são tão claramente abordadas quanto as medidas de localização, como média mediana e moda. No entanto, configuram-se como ferramentas de grande utilidade, ao passo que nos permitem obter insigths a respeito do nosso conjunto de dados, principalmente no que se refere a sua distribuição.
As medidas de dispersão são utilizadas para caracterizar a variabilidade de nossos dados, algo que as medidas de localização não nos apresentam. Se tivermos, por exemplo, um conjunto de dados expresso por , verificamos que sua média equivale a 50. Da mesma forma, para o conjunto de dados , sua média equivale a 50. Assim, percebemos que mesmo diante de uma variabilidade maior no primeiro conjunto, as médias são equivalentes, ou seja, é obtido um padrão de comportamento central, mas, somente por meio da média, não conseguimos compreender o comportamento da distribuição do nosso conjunto de dados.
É de grande relevância, portanto, trabalharmos com medidas de tendência central e medidas de dispersão de forma conjunta, ao passo que a sinergia entre elas nos permite obter características de comportamento, tanto em termos centrais quanto em termos de variabilidade.
Uma das principais medidas de dispersão é a amplitude, que determina a diferença entre os valores das duas extremidades de um conjunto de dados, ou seja, trata-se da subtração do valor máximo pelo valor mínimo. Seja . Temos que e . A amplitude é obtida por:
A amplitude, por si só, não é uma medida de dispersão muito clara, especialmente quando trabalhamos com um conjunto de dados único. O valor obtido no caso anterior, por exemplo, nos indica que a amplitude está próxima do valor máximo, mas não muito além disso. Para que se possa obter uma medida de variação de melhor interpretação, é necessário estabelecer um valor de referência, como a média. Quando avaliamos a distância de cada observação de um conjunto para sua respectiva média, trabalhamos com o conceito de desvio médio absoluto, expresso por:
Estamos calculando, portanto, a variação de cada observação em relação à média. Suponha que represente um vetor de dados, tal que . A média do vetor é dada por . Dessa forma, os desvios obtidos são obtidos conforme a Tabela 2.6.
Tabela 2.6 | Desvios do vetor de dados apresentado
Fonte: elaborada pelo autor.
| 1 | -2 | 2 |
| 2 | -1 | 1 |
| 3 | 0 | 0 |
| 4 | 1 | 1 |
| 5 | 2 | 2 |
Observamos que o maior desvio, considerando o valor absoluto, é obtido em e . Para calcularmos o desvio médio absoluto, basta realizarmos a soma absoluta dos desvios e dividir pelo total de observações. No exemplo, .
O cálculo dos desvios oferece os insumos necessários para discutirmos uma das medidas de dispersão mais importantes: a variância. De forma geral, a variância avalia a proximidade das observações com a média do conjunto de dados. Quanto maior seu valor, mais dispersos e distantes os dados se encontram.
Existem dois cálculos possíveis para a variância: a amostral e a populacional (BUSSAB; MORETTIN, 2010). A variância amostral é dada por:
De forma similar, a variância populacional é expressa por:
Note que ambas as fórmulas apresentam um numerador comum (soma dos quadrados dos desvios). No entanto, os denominadores variam conforme a variância amostral ou populacional (TRIOLA, 2008). No dia a dia, dificilmente trabalharemos com dados populacionais, pois isso exigiria obter observações de todas as pessoas de interesse. É comum a operação com dados amostrais que, quando bem amostrados, representam o comportamento da população. Logo, a fórmula da variância normalmente utilizada é a amostral.
Suponha que uma consultoria de mercado esteja avaliando o faturamento anual de dez empresas do setor de energia elétrica. Os dados coletados foram dispostos na Tabela 2.7.
Tabela 2.7 | Faturamento anual das empresas avaliadas (R$ milhões)
Fonte: elaborada pelo autor.
| Empresa | Faturamento Anual (R$ milhões) |
|---|---|
| Empresa A | 450 |
| Empresa A | 410 |
| Empresa C | 360 |
| Empresa D | 220 |
| Empresa F | 350 |
| Empresa G | 450 |
| Empresa H | 330 |
| Empresa I | 435 |
| Empresa J | 115 |
| Empresa K | 360 |
Considerando os faturamentos apresentados, temos um total de R$ 3.840 mi para todas as lojas, o que confere ao grupo uma média equivalente a R$ 348 mi. Com a média em mãos, é possível calcular os desvios e os quadrados dos desvios, conforme apresentado na Tabela 2.8, em que a variável “Faturamento Anual (R$ mi)” foi alterada para x.
Tabela 2.8 | Desvios e quadrados dos desvios do faturamento das empresas
Fonte: elaborada pelo autor.
| Empresa | |||
|---|---|---|---|
| Empresa A | 450 | 102 | 10.404 |
| Empresa B | 410 | 62 | 3.844 |
| Empresa C | 360 | 12 | 144 |
| Empresa D | 220 | -128 | 16.384 |
| Empresa F | 350 | 2 | 4 |
| Empresa G | 450 | 102 | 10.404 |
| Empresa H | 330 | -18 | 324 |
| Empresa I | 435 | 87 | 7.569 |
| Empresa J | 115 | -233 | 54.289 |
| Empresa K | 360 | 12 | 144 |
| Total | 3.480 | 0 | 103.510 |
Obtivemos, portanto, o numerador para o cálculo da variância populacional, equivalente à soma dos quadrados dos desvios. No exemplo, o valor total foi de 103.510. Assim, para calcularmos a variância amostral, devemos dividir o numerador obtido por . Como o levantamento apresenta dez empresas, . Desse modo, a variância amostral é dada por:
A variância é uma métrica importante, porém sua interpretabilidade está em termos comparativos. No exemplo anterior, se o faturamento da empresa H fosse R$ 1.000 milhões, a variância total saltaria para 53.711,11. Ao compararmos os dois valores, notamos que este último é quase cinco vezes superior ao obtido anteriormente, indicando que um conjunto apresenta maior variabilidade do que o outro.
O cálculo da variância nos permite apresentar outra medida de dispersão, o desvio padrão. De forma geral, o desvio padrão indica quanto os valores de um conjunto estão distribuídos em relação a sua média. Quanto maior o desvio, mais distribuídos estarão os dados. Quanto menor, mais concentradas estarão as observações em torno da média.
Para melhor compreendermos o comportamento do desvio padrão, a Figura 2.1 apresenta dois gráficos oriundos de simulações. Ambos apresentam média e . A diferença reside no desvio padrão, que equivale a 1 e 5, nos gráficos da esquerda e direita, respectivamente. Na interpretação da distribuição é necessária uma análise cuidadosa. Quando olhamos o histograma com desvio padrão igual a 5, os dados parecem mais concentrados do que no histograma com desvio padrão igual a 1. No entanto, ao observarmos os eixos de ambos os gráficos, é possível perceber que um desvio padrão maior está associado a valores mais dispersos.
O cálculo do desvio padrão é relativamente simples. Encontrada a variância, basta tirar a raiz quadrada de seu respectivo valor (BUSSAB; MORETTIN, 2010). Assim, quando falamos de variância amostral , o desvio padrão é obtido por:
Considerando o exemplo dos faturamentos das empresas, em que foi obtida uma variância de 11.501,11, o desvio padrão equivale a .
Exemplificando
Os investimentos em ações são considerados de alto risco em função da volatilidade associada ao comportamento dos preços. Quanto maiores as oscilações, mais alto será o valor da variância. Por essa razão, ativos com alta variância e desvio padrão são considerados investimentos de alto risco, ou seja, é possível perder muito dinheiro, mas também é possível obter retornos acima da média do mercado.
Por fim, outra importante medida de dispersão é a covariância. Enquanto a variância avalia o comportamento de uma única variável em relação a sua média, a covariância considera um comportamento conjunto, ou seja, trabalha com a dispersão de duas variáveis em relação a suas respectivas médias.
Sejam x e y duas variáveis quaisquer. A covariância é dada por:
Considere que ao mesmo exemplo do faturamento das empresas foi inserido um novo dado, referente ao número de colaboradores. O novo conjunto é apresentado na Tabela 2.9.
Tabela 2.9 | Faturamento e quantidade de funcionários das empresas levantadas
Fonte: elaborada pelo autor.
| Faturamento Anual (R$ mi) | Funcionários |
|---|---|
| 450 | 3.100 |
| 410 | 4.200 |
| 360 | 3.100 |
| 220 | 3.300 |
| 350 | 3.200 |
| 450 | 4.500 |
| 330 | 3.200 |
| 435 | 4.800 |
| 115 | 2.100 |
| 360 | 3.000 |
| 3.480 | 34.500 |
Como forma de facilitar os cálculos, substituiremos as variáveis “Faturamento Anual (R$ mi)” e “Funcionários” por e , respectivamente. Nesse sentido, tem-se que e . A partir da Tabela 2.10, calculamos os desvios de cada variável, bem como a produto desses desvios, cujo somatório nos permitirá calcular a covariância.
Tabela 2.10 | Cálculos para a obtenção da covariância
Fonte: elaborada pelo autor.
| Empresa | |||||
|---|---|---|---|---|---|
| Empresa A | 450 | 3.100 | 102 | -350 | -35.700 |
| Empresa B | 410 | 4.200 | 62 | 750 | 46.500 |
| Empresa C | 360 | 3.100 | 12 | -350 | -4.200 |
| Empresa D | 220 | 3.300 | -128 | -150 | 19.200 |
| Empresa F | 350 | 3.200 | 2 | -250 | -500 |
| Empresa G | 450 | 4.500 | 102 | 1.050 | 107.100 |
| Empresa H | 330 | 3.200 | -18 | 250 | 4.500 |
| Empresa I | 435 | 4.800 | 87 | 1.350 | 117.450 |
| Empresa J | 115 | 2.100 | -233 | -1.350 | 314.550 |
| Empresa K | 360 | 3.000 | 12 | -450 | -5.400 |
| Total | 3.480 | 34.500 | 0 | 0 | 563.500 |
Assim, a covariância de e é dada por:
O valor de 62.611,11 indica uma relação de tendência positiva entre as variáveis, ou seja, quando uma aumenta, a outra também varia positivamente. Esse efeito de tendência pode ser observado na Figura 2.2, que apresenta um gráfico de dispersão das variáveis analisadas.
A partir do gráfico de dispersão apresentado, é possível observar a relação positiva existente entre as duas variáveis.
Um importante artifício na análise de dispersão é a matriz de variâncias e covariâncias. De modo geral, a dimensão da matriz varia de acordo com o número de variáveis. Suponha que estejamos trabalhando com um conjunto de dados de cinco variáveis. A matriz de variâncias e covariâncias terá dimensão 5x5, conforme apresentado no Quadro 2.1.
Quadro 2.1 | Exemplo de Matriz de Variâncias e Covariâncias
Fonte: elaborado pelo autor.
Dessa forma, é possível observar que os elementos da diagonal da matriz representam as variâncias de cada uma das variáveis, enquanto os demais elementos compreendem as covariâncias.
Assimile
A matriz de variâncias e covariâncias apresenta, por natureza, um padrão de simetria, ou seja, os elementos acima da sua diagonal são equivalentes aos elementos que estão abaixo. Isso ocorre pelo fato de a covariância não depender da ordem em que a relação é estabelecida, ou seja,
Para fixarmos os conteúdos apresentados nesta seção, trabalharemos com um exemplo que contemple todas as medidas abordadas. Suponha, portanto, que uma empresa esteja avaliando o desempenho de suas unidades de venda. Para tanto, foram coletadas, junto aos clientes, notas a respeito de cinco categorias: preço, prazo, atendimento, entrega e pós-venda. Os valores médios de cada unidade foram obtidos e computados conforme a Tabela 2.11.
Tabela 2.11 | Médias das notas das unidades por quesito
Fonte: elaborada pelo autor.
| Unidade | Preço | Prazo | Atendimento | Entrega | Pós-Venda |
|---|---|---|---|---|---|
| A | 5,1 | 8,0 | 8,1 | 5,1 | 8,0 |
| B | 7,8 | 8,0 | 8,1 | 8,0 | 6,1 |
| C | 8,1 | 7,1 | 5,0 | 5,0 | 6,1 |
| D | 6,0 | 9,0 | 7,1 | 5,1 | 6,1 |
| E | 8,1 | 6,0 | 6,1 | 7,0 | 6,1 |
| F | 8,0 | 6,0 | 9,1 | 7,1 | 6,0 |
| G | 8,0 | 9,0 | 7,1 | 8,1 | 8,0 |
| H | 9,0 | 6,0 | 8,0 | 8,0 | 7,0 |
| I | 7,1 | 6,0 | 9,0 | 8,0 | 5,0 |
| J | 9,0 | 8,1 | 7,0 | 7,0 | 5,1 |
| Total | 76,2 | 73,2 | 74,6 | 68,4 | 63,5 |
Com auxílio do R, obteremos a amplitude, o desvio médio absoluto, a variância e o desvio padrão das variáveis individualmente, além das covariâncias entre as variáveis, tomadas duas a duas.
Para as avalições por variável, os resultados obtidos devem seguir os valores apresentados na Tabela 2.12.
Tabela 2.12 | Principais medidas-resumo obtidas
Fonte: elaborada pelo autor.
| Medida | Preço | Prazo | Atendimento | Entrega | Pós-Venda |
|---|---|---|---|---|---|
| Média | 7,6 | 7,3 | 7,5 | 6,8 | 6,4 |
| Mediana | 8,0 | 7,6 | 7,6 | 7,1 | 6,1 |
| Variância | 1.5 | 1,6 | 1,6 | 1,7 | 1,1 |
| Amplitude | 3,9 | 3,0 | 4,1 | 3,1 | 3,0 |
| Desvio Médio Abs. | 0,9 | 1,1 | 1,0 | 1,1 | 0,8 |
| Desvio Padrão | 1,2 | 1,3 | 1,3 | 1,3 | 1,0 |
Por outro lado, para as covariâncias, devem ser obtidos os valores presentes no Quadro 2.2.
Quadro 2.2 | Matriz de variâncias e covariâncias dos quesitos
Fonte: elaborado pelo autor.
| Preço | Prazo | Atendimento | Entrega | Pós-Venda | |
|---|---|---|---|---|---|
| Preço | 1,5 | -0,6 | -0,3 | 0,9 | -0,4 |
| Prazo | -0,6 | 1,6 | -0,4 | -0,5 | 0,5 |
| Atendimento | -0,3 | -0,4 | 1,6 | 0,8 | 0,0 |
| Entrega | 0,9 | -0,5 | 0,8 | 1,7 | -0,1 |
| Pós-Venda | -0,4 | 0,5 | 0,0 | 0,1 | 1,1 |
Medidas de Dispersão
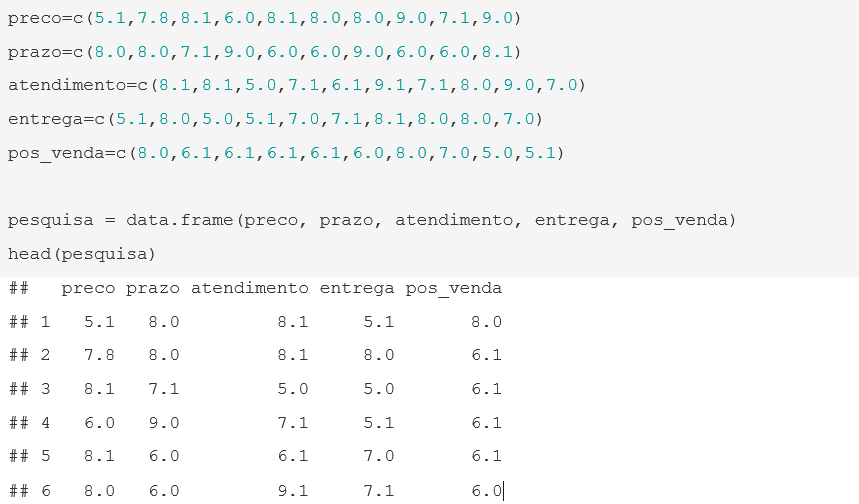
Prezado estudante, neste momento trabalharemos com um exercício prático de aplicação das medidas de dispersão. Para tanto, daremos continuidade ao exemplo apresentado no corpo do texto, em que uma empresa está avaliando as notas atribuídas pelos clientes para cada um dos cinco componentes destacados: preço, prazo, atendimento, entrega e pós-venda.
O primeiro passo é gerar as variáveis apresentadas. Para tanto, utilizaremos os comandos c() e data.frame(). Note que utilizamos . (ponto) para indicar as casas decimais, em vez de , (vírgula).
Em seguida, obteremos as amplitudes das variáveis. Para tanto, utilizamos os comandos min() e max().
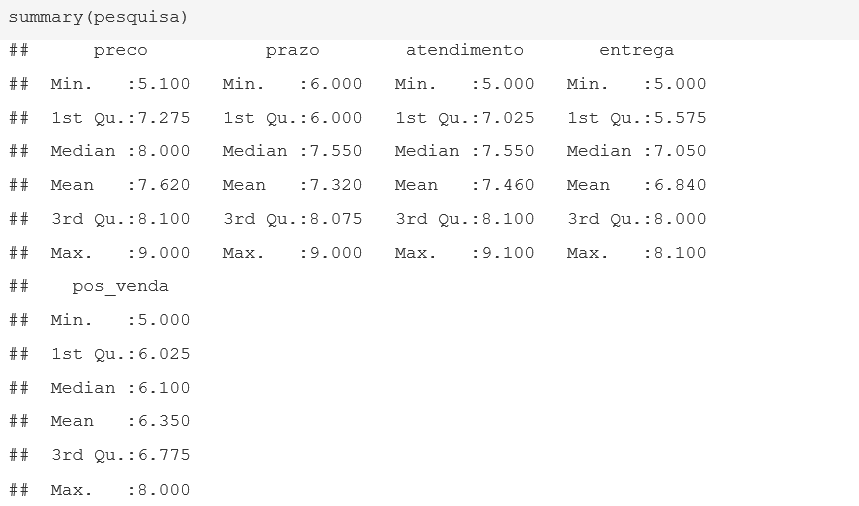
Para obtermos a média e a mediana, podemos utilizar o comando summary(), que nos trará um breve resumo estatístico dos dados.
O desvio médio absoluto será obtido por meio da própria fórmula:
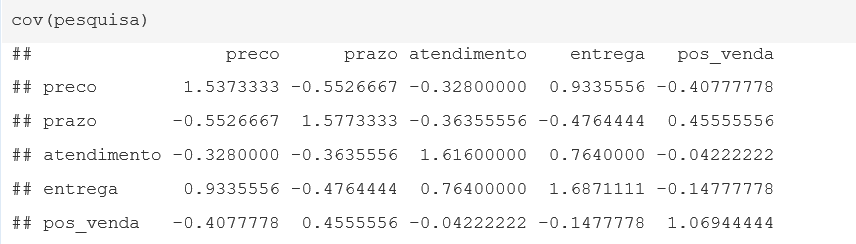
Por fim, para o cálculo das variâncias e covariâncias, utilizaremos a matriz de variâncias e covariâncias, obtida pelo comando cov.
Agora faça você mesmo os testes utilizando o compilador a seguir:
Para visualizar o vídeo, acesse seu material digital.
É possível perceber, portanto, que a menor variação entre as unidades foi observada no quesito pós-venda, o que não é algo necessariamente bom. Quando olhamos para a média, o pós-venda obteve um valor de 6,4, o menor entre os cinco quesitos. Houve pouca variação, porém em torno de uma baixa média.
Reflita
Avalie as demais variáveis e seus respectivos comportamentos. Perceba que, embora uma variável possa ter um “bom comportamento” em uma medida específica, isso não significa que ela apresenta um bom desempenho, conforme vimos no quesito pós-venda.
Com o exemplo apresentado, encerramos o conteúdo teórico da seção, dando mais um passo para a formação em análise de dados. As medidas de dispersão certamente farão parte de sua atividade profissional. Portanto, é sugerida exploração de todos os recursos disponíveis nesta seção, como forma de fortalecer o aprendizado.
Faça a valer a pena
Questão 1
Uma agroindústria do setor de grãos está avaliando o peso das sacas de soja. Cada saca tem 60 kg de capacidade. No entanto, após realizar a pesagem com uma balança de maior precisão, a empresa identificou uma variância de 6,25.
Com base no valor obtido, assinale a alternativa que apresenta corretamente o valor equivalente ao desvio padrão da pesagem realizada pela empresa.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Correto!
O exercício apresenta o cálculo da variância e solicita, a partir do valor informado, que se encontre o desvio padrão. Considerando que o desvio padrão equivale à raiz quadrada da variância, tem-se que o valor correto é
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Questão 2
Uma empresa está avaliando a relação entre as variações de funcionários e as variações do faturamento, em um período de seis anos. Para tanto, o proprietário tabulou os dados e os dispôs conforme tabela que segue.
Tabela | Faturamento anual e quantidade de funcionários
Fonte: elaborada pelo autor.
| Ano | Faturamento | Funcionários |
|---|---|---|
| Ano 1 | 110.000,00 | 13 |
| Ano 2 | 120.000,00 | 15 |
| Ano 3 | 125.000,00 | 16 |
| Ano 4 | 125.000,00 | 18 |
| Ano 5 | 130.000,00 | 14 |
| Ano 6 | 140.000,00 | 18 |
Com base nos valores apresentados, assinale a alternativa que apresente corretamente a covariância amostral entre as variáveis faturamento e funcionários.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Correto!
A resolução da questão envolve a aplicação do cálculo da covariância. Considerando a tabela apresentada, obtém-se como suporte a seguinte relação:
Com o somatório do produto dos desvios em mãos, é necessário dividir o valor obtido por . Assim, a covariância entre as variáveis faturamento e funcionários é dada por: .
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Questão 3
De janeiro a maio, a quantidade de vendas de uma empresa do setor do varejo foi equivalente a 1.150 unidades, distribuídas conforme tabela a seguir:
Tabela | Evolução da quantidade de vendas da empresa (janeiro a maio)
Fonte: elaborada pelo autor.
| Mês | Quantidade de vendas |
|---|---|
| Jan | 250 |
| Fev | 350 |
| Mar | 150 |
| Abr | 250 |
| Mai | 150 |
Considerando as quantidades informadas, assinale a alternativa que apresenta os valores da variância e do desvio padrão dos dados em questão. Considere a variância amostral para o cálculo.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Correto!
A resolução da questão passa pelo cálculo dos valores da média, variância e desvio padrão. Para tanto, é importante que se abram colunas adicionais na tabela informada, com o cálculo dos desvios e do quadrado dos desvios, conforme a tabela que segue.
Com a soma dos quadrados dos desvios em mãos, basta dividir o valor encontrado por para encontrar a variância dos dados. Logo, tem-se que . Assim, para o cálculo do desvio padrão, deve-se extrair a raiz quadrada da variância, o que equivale a 83,67 (arredondado para duas casas decimais).
A alternativa correta é 7.000 e 83,67.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Referências
BUSSAB, W. de O.; MORETTIN, P. A. Estatística básica. In: BUSSAB, W. de O.; MORETTIN, P. A. Estatística básica. São Paulo: Saraiva, 2010. p. xvi, 540-xvi, 540.
LÚCIO, A. D. et al. Variância e média da massa de frutos de abobrinha-italiana em múltiplas colheitas. Horticultura Brasileira, v. 26, n. 3, p. 335-341, 2008.
TRIOLA, M. F.; IOSSI, L. Essentials of statistics. Boston, MA, USA: Pearson Addison Wesley, 2008.