Integração numérica

lorem ipsum dolor sit amet

Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nunc dignissim euismod urna tincidunt sagittis. Vivamus id vehicula eros, non scelerisque eros.

Fonte: Shutterstock.

Deseja ouvir este material?

Áudio disponível no material digital.

praticar para aprender

Caro aluno, nesta seção vamos trabalhar basicamente com dois tópicos: regra dos trapézios e regra de Simpson. Ambos os tópicos são ferramentas para aproximar o valor de uma integral, consequentemente de uma área, usando métodos numéricos. Essas ferramentas são importantes, pois, na prática, raramente temos figuras regulares ou até mesmo funções bem-comportadas. A maioria dos problemas são resolvidos usando métodos numéricos devido à versatilidade desses métodos. Imagine só ter que lidar com a modelagem do crescimento populacional ou até mesmo o aumento dos casos de Covid-19 sem fazer o uso de métodos numéricos. Seria extremamente complexo! 
Em um estudo envolvendo Engenharia Biomédica, um determinado pesquisador realizou um trabalho voltado para modelagem de marca-passo no coração de pessoas idosas. Em sua pesquisa, ele tinha por interesse achar a área abaixo da curva gerada pelos dados do marca-passo. Sabe-se que a função que governa o marca-passo é descrita por:
$f\left(x\right)=\mathrm{0,3}+20x-140x²+730x³-810x^4+200x^5$
no intervalo de 0,2 até 0,8 horas. Uma vez que ele tiver a área abaixo dessa curva e sabendo que essa função tem certos padrões de repetição, ele conseguirá estimar a área total para mais do que 0,6 horas, considerada em seu experimento para avaliar a qualidade do marca-passo. Então, baseando-se nos conceitos de integração numérica, como você calcularia a área abaixo da função dada assumindo uma margem de erro de no máximo 1%? 
Conseguiu ver a importância desses conceitos? Que tal começarmos a trabalhar com eles e entender melhor sob o ponto de vista matemático e prático? Não se preocupe, vamos lhe acompanhar em todo o processo e os conceitos serão construídos de forma gradual! 

conceito-chave

Já vimos anteriormente como trabalhar com os erros de aproximações e também com formas de resolver a equação $f\left(x\right)=0$. Agora, nos interessa saber como resolver numericamente as integrais, uma vez que elas, assim como a equação $f\left(x\right)=0$, têm diversas aplicações em Engenharia, como no cálculo aproximado da área de placas de metais em construção civil. Nesse aspecto, a ideia da integração numérica consiste, basicamente, na aproximação da função integranda $f$ por um polinômio em que a escolha desse polinômio e dos pontos usados em sua determinação vai resultar nos diversos métodos numéricos de integração. 
Em Cálculo Diferencial e Integral, é visto que as fórmulas de integração numéricas são somatórios, em que suas parcelas são, necessariamente, valores de $f\left(x\right)$ calculados em pontos escolhidos e multiplicados por pesos convenientes, isto é,
${\int }_a^{b}f\left(x\right)dx\approx {\sum }_{i=0}^n{\omega }_{i}f\left(x_i\right)$
onde $a \le x_0 < x_1 < . . . < x_n \le b$ são pontos de integração e os ${\omega }_i$ são os pesos. Então, para iniciar nossos estudos, nesta seção vamos considerar apenas as fórmulas fechadas, isto é, os extremos de integração coincidem com $x_0$ e $x_n$. 
Dessa forma, dada uma função $f : \left[a, b\right] \to ℝ$, seja $n$ um número natural e $h =\frac{b – a}{n}$, dizemos que os pontos $x_j=x_0+j_h, j =\mathrm{0,} \mathrm{1,} . . . , n$ são igualmente espaçados (ANDRADE, 2012). Assim, seja $P_n\left(x\right)$ o polinômio de grau $$\begin{gathered} n \\ h =\frac{b – a}{n} \end{gathered}$$ que interpola os pontos $\left(x_i, f\left(x_i\right)\right), i = \mathrm{0,} \mathrm{1,} . . . , n$. Pelo método de interpolação de Lagrange, sabemos que:
$P_n\left(x\right)= {\sum }_{i=0}^{n}f\left(x_i\right)L_i\left(x\right)$
e o erro:
$f\left(x\right)- P_{n\left(x\right)}=\frac{f\left(n+1\right)\left(\alpha \right)}{\left(n + 1\right)!}\left(x - x_0\right)\left(x - x_1\right). . . \left(x - x_n\right),$
onde $\alpha = \alpha \left(x\right)$ é um ponto em $\left(a, b\right)$. Assim, integrando em $\left(a, b\right)$, obtemos que:
${\int }_a^{b}f\left(x\right)dx={\sum }_{i=0}^{n}f\left(x_i\right){\int }_a^b{L}_i\left(x\right)dx+{\int }_a^b\frac{f\left(n+1\right)\left(\alpha \right)}{\left(n + 1\right)!}\left(x - x_0\right)\left(x - x_1\right) . . . \left(x - x_n\right)dx,$
onde $\alpha = \alpha \left(x\right)$ é um ponto em $\left(a, b\right)$. Nesse caso, podemos chamar:
${\omega }_i={\int }_a^b{L}_i\left(x\right)dx$
a fim de simplificar a expressão de ${\int }_a^{b}f\left(x\right)dx$ como:
${\int }_a^{b}f\left(x\right)dx={\sum }_{i=0}^n{\omega }_{i}f\left(x_i\right)+{\int }_a^b\frac{f\left(n+1\right)\left(\alpha \right)}{\left(n + 1\right)!}\left(x - x_0\right)\left(x - x_1\right) . . . \left(x - x_n\right)dx$,
que é conhecida como fórmula de Newton-Cotes para integrais numéricas. Como caso particular dessa fórmula, obtemos as famosas fórmulas dos trapézios e de Simpson, que são estabelecidas com polinômios de grau 1 e grau 2, respectivamente. Vamos iniciar então com a fórmula dos trapézios, ou regra dos trapézios.
A fórmula dos trapézios corresponde, basicamente, à interpolação da função a ser integrada por um polinômio de grau 1 (ANDRADE, 2012). A interpolação linear, nesse caso, necessita de dois pontos, então, vamos trabalhar com os extremos do intervalo de integração, isto é, $a = x_0$ e $b = x_1$. Logo, o polinômio linear interpolador é dado por:
$$\begin{gathered} p_1\left(x\right)= y_0 \frac{x - x_1}{x_0- x_1} + y_1\frac{x - x_0}{x_1- x_{0 \\ }} \end{gathered}$$
em que $y_0=f\left(x_0\right),y_1=f\left(x_1\right)$ são as coordenadas de y. E os pesos são dados por:
${\omega }_0 ={\int }_{x_0}^{x_1} \frac{x - x_1}{x_0- x_1}dx=\frac{h}{2},$
${\omega }_1 ={\int }_{x_0}^{x_1} \frac{x - x_0}{x_1- x_0}$
Para uma melhor visualização dessa ideia, vamos trabalhar com o gráfico exposto na Figura 2.1.

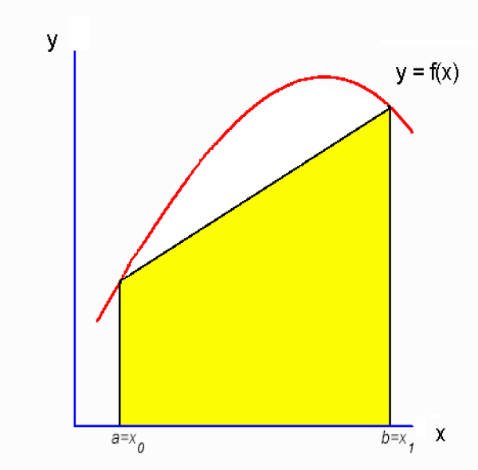
Assim, observando a Figura 2.1 e partindo dos pesos, temos que:
${\int }_{x_0}^{x_1}f\left(x\right)dx=\frac{h}{2}f\left(x_0\right)+\frac{h}{2}f\left(x_1\right)+erro$,
onde o erro é descrito pela seguinte equação:
$E_T=\frac{1}{2} {\int }_{x_1}^{x_0}{f}^{\text{'}\text{'}}\left(\alpha \right)\left(x - x_0\right)\left(x - x_1\right)dx,$
onde $\alpha = \alpha x$ é um ponto entre $x_0$ e $x_1$. Agora, usando o teorema do valor médio para integrais, obtemos que existe $\beta \in \left(x_0, x_1\right)$, tal que:
$E_T=\frac{1}{2} {\int }_{x_1}^{x_0}{f}^{\text{'}\text{'}}\left(\alpha \right)\left(x - x_0\right)\left(x - x_1\right)dx=-\frac{f^{\text{'}\text{'}}\left(\beta \right)h^3}{12}$
Portanto, podemos escrever a fórmula dos Trapézios para integração numérica como:
${\int }_{x_0}^{x_1}f\left(x\right)dx=\frac{h}{2}f\left(x_0\right)+\frac{h}{2}f\left(x_1\right)-\frac{f^{\text{'}\text{'}}\left(\beta \right)h^3}{12}$,
onde $\beta \in \left(a, b\right)$ não é conhecido.

Vimos então como resolvemos a regra dos Trapézios usando um polinômio interpolador de grau 1. E para a regra de Simpson, como procedemos? Nesse caso, vamos interpolar $f\left(x\right)$ usando um polinômio de grau 2 que coincida com essa função em $x_1=\frac{a + b}{2}$,  e $b = x_2$. Assim, o polinômio interpolador de grau 2 é dado pela equação:
$p_2\left(x\right)= y_0\frac{\left(x – x_1\right)\left(x – x_2\right)}{\left(x_0– x_1\right)\left(x_0– x_2\right)}+ y_1\frac{\left(x – x_0\right)\left(x – x_2\right)}{\left(x_1– x_0\right)\left(x_1– x_2\right)}+ y_2\frac{\left(x – x_0\right)\left(x – x_1\right)}{\left(x_2– x_0\right)\left(x_2– x_1\right)}.$
em que $y_0=f\left(x_0\right),y_1=f\left(x_1\right),y_2=f\left(x_2\right)$ são as coordenadas de y. Para uma melhor visualização dessa ideia, vamos trabalhar com o gráfico exposto na Figura 2.2.

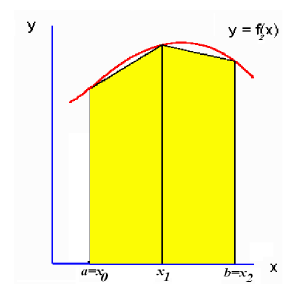
Dessa forma, a partir dos polinômios de Lagrange, obtemos os pesos da fórmula de Simpson:
${\omega }_0={\int }_{x_0}^{x_2} \frac{\left(x - x_1\right)\left(x-x_2\right)}{\left(x_0- x_1\right)\left(x_0-x_2\right)}dx=\frac{h}{3}$
${\omega }_1={\int }_{x_0}^{x_2} \frac{\left(x - x_0\right)\left(x-x_2\right)}{\left(x_1- x_0\right)\left(x_1-x_2\right)}dx=\frac{h}{3}$
${\omega }_2={\int }_{x_0}^{x_2} \frac{\left(x - x_0\right)\left(x-x_1\right)}{\left(x_2- x_0\right)\left(x_2-x_1\right)}dx=\frac{h}{3}$
Assim, obtemos a seguinte solução para a integral:
 ${\int }_{x_0}^{x_2}f\left(x\right)dx=\frac{h}{3}\left[f\left(x_0\right)+4f\left(x_1\right)+f\left(x_2\right)\right]+erro$,
onde o erro é dado pela seguinte expressão:
$E_S=\frac{1}{3!}{\int }_{x_0}^{x_1}{f}^{\left(3\right)}\left(\alpha \right)\left(x – x_0\right)\left(x – x_1\right)\left(x – x_2\right)dx= -\left[\frac{h^5}{90}\right]f^{\left(4\right)}\left(\beta \right)$
para algum $\beta \in \left(x_0, x_2\right)$. Portanto, a fórmula de Simpson para integração numérica é descrita pela equação:
${\int }_{x_0}^{x_2}f\left(x\right)dx=\frac{h}{3}\left[f\left(x_0\right)+4f\left(x_1\right)+f\left(x_2\right)\right]+-\left[\frac{h^5}{90}\right]f^{\left(4\right)}\left(\beta \right)$

Agora, vamos avaliar outros aspectos dessas fórmulas: intervalos de integração grandes. Quando o intervalo de integração é grande, em geral, não é conveniente aumentar o grau do polinômio interpolador para obter fórmulas mais precisas, pois podemos deixar o problema ainda mais complexo. A alternativa mais usada é subdividir o intervalo de integração e aplicar fórmulas simples repetidas vezes, obtendo-se as fórmulas compostas. Vamos começar com a regra dos trapézios composta.
Nesse caso, de acordo com Andrade (2012), dado o intervalo $\left[a, b\right]$ dividindo-o em $n$ subintervalos de comprimento $h =\frac{b – a}{n}$ e fazendo $x_0 = a$, $x_i = x_0 + ih$, $i = \mathrm{0,} \mathrm{1,} . . . , n$ e $x_n=b$, obtemos:
${\int }_a^{b}f\left(x\right)dx={\sum }_{i=1}^n{\int }_{x_{i-1}}^{x_i}f\left(x\right)dx$$={\int }_{x_0}^{x_1}f\left(x\right)dx+{\int }_{x_1}^{x_2}f\left(x\right)dx+\dots +{\int }_{x_{n-1}}^{x_n}f\left(x\right)dx$
$\approx \frac{h}{2}\left[f\left(x_0\right)+f\left(x_1\right)\right]+\frac{h}{2}\left[f\left(x_1\right)+f\left(x_2\right)\right]+\dots +\frac{h}{2}\left[f\left(x_{n-1}\right)+f\left(x_n\right)\right]$
$\approx \frac{h}{2}\left[f\left(x_0\right)+2{\sum }_{i=1}^{n-1}f\left(x_i\right)+f\left(x_n\right)\right].$
que é chamada de fórmula composta para a regra dos trapézios. Nesse caso, o erro final dessa fórmula tem como base os erros parciais da fórmula simples dos trapézios que são dados por:
$-\frac{h^3}{12}f’’\left({\beta }_i\right)$
Logo, o erro final é dado por:
$E_{Tc}=-\frac{h^3}{12}\left[f’’\left({\beta }_1\right)+f’’\left({\beta }_2\right)+ · · ·+ f’’\left({\beta }_n\right)\right]$
Isto é,
$\left|E_{Tc}\right|\le \left(b-a\right)\frac{h^3}{12}\sup \left\{\left|f^{\text{'}\text{'}}\left(x\right)\right|; x\in \left[a,b\right]\right\}$
E para a regra de Simpson, como procedemos? Nesse caso, dado o intervalo $\left[a, b\right]$ dividindo-o em $n$ subintervalos de comprimento $h =\frac{b – a}{n}$ e fazendo $x_0=a$, $x_i=x_0+ih, i = \mathrm{0,} \mathrm{1,} . . . , n$ e $x_n=b$, obtemos:
${\int }_a^{b}f\left(x\right)dx={\int }_{x_0}^{x_2}f\left(x\right)dx+{\int }_{x_2}^{x_4}f\left(x\right)dx+\dots +{\int }_{x_{n-2}}^{x_n}f\left(x\right)dx$
$\approx \frac{h}{3}\left[f\left(x_0\right)+4f\left(x_1\right)+f\left(x_2\right)\right]+\dots +\frac{h}{3}\left[f\left(x_{n-2}\right)+4f\left(x_{n-1}\right)+f\left(x_n\right)\right]$
$\approx \frac{h}{3}[f\left(x_0\right)+4{\sum }_{i=1}^{\frac{n}{2}}f\left(x_{2i-1}\right)+2{\sum }_{i=1}^{\frac{n-2}{2}}f\left(x_{2i}\right)+f\left(x_n\right)$
que é conhecida como fórmula composta para a regra de Simpson. Da mesma forma que na regra dos trapézios composta, o erro final da regra composta de Simpson pode ser obtido pela soma dos erros parciais. Portanto, o erro final da regra composta de Simpson é dado por:
$\left|E_{Sc}\right|\le \left(b - a\right)\frac{h^4}{180}\max \left\{\left|f^{\left(4\right)}\left(x\right)\right|; x \in \left[a, b\right]\right\}$

Para finalizar nosso estudo de integração numérica, vamos trabalhar com um exemplo de cálculo de integral com base nas regras de Simpson e dos trapézios com erro menor que ${10}^{-4}$.

Como exercício prático, você pode escrever a aproximação da integral considerando pela regra de Simpson e pela regra dos trapézios usando 6 intervalos. Para finalizar, deixo a reflexão: qual desses métodos é mais viável quando eu tenho uma integral mais complexa?

Faça a valer a pena

Referências

ANDRADE, D. Cálculo numérico. In: NOTAS de aula. [S. l.], 2012.
FERNANDES, D. B. Cálculo Numérico. São Paulo: Editora Pearson, 2015.
FRANCO, N. B. Cálculo Numérico. São Paulo: Editora Pearson, 2006.
HFM. Integração Numérica. CN15. 2010. Disponível em: https://homepages.dcc.ufmg.br/~hfmatos/CN/mirlaine/aula15.pdf. Acesso em: 26 mar. 2021.