lorem ipsum dolor sit amet
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nunc dignissim euismod urna tincidunt sagittis. Vivamus id vehicula eros, non scelerisque eros.

Fonte: Shutterstock.
Deseja ouvir este material?
Áudio disponível no material digital.
Convite ao estudo
Caro aluno, você sabia que uma das melhores maneiras de representar dados é com gráficos e tabelas? E fazendo esse tipo de representação, você está trabalhando com estatística? Nesta unidade, vamos trabalhar com os principais conceitos de estatística, iniciando-se com a estatística descritiva e os principais tipos de gráficos. Logo em seguida, vamos revisar algumas definições de população e amostra, além dos conceitos de probabilidade. No entanto, nosso foco será trabalhar com resumo de dados e cálculos de probabilidades condicionais que são amplamente utilizados em testes de diagnósticos e também para encontrar o padrão-ouro, que é fundamental para comparação de parâmetros. Por fim, vamos entender os testes de hipóteses, que são fundamentais quando o assunto é tomar uma decisão. Vamos entender todos os fatores que afetam uma tomada de decisão e como decidir, estatisticamente falando.
Algo que você pode estar se perguntando é: mas como utilizamos a estatística em áreas como a Engenharia? Para exemplificar, suponha que você trabalhe com energia eólica e seu patrão te faça tomar uma decisão se este tipo de energia é útil e se vai gerar lucros e ser sustentável. O que você faria? Naturalmente, você coletaria dados e elaboraria uma hipótese que seria validada por métodos estatísticos para apresentar seus resultados e apresentaria gráficos. Viu como a estatística é importante nesse aspecto? Para lhe auxiliar, vamos, no decorrer desta unidade, aprender um pouco mais sobre ela! Então, mãos à obra!
Praticar para aprender
Nesta seção, iremos entender como construir gráficos e tabela e como trabalhar com isso na prática. Esses conceitos são fundamentais, uma vez que são úteis para resumir informações e gerar apresentações a comitês sobre os resultados.
Como exemplo dessa abordagem, podemos considerar que você tenha interesse em lançar um serviço no mercado. Para isso, você deve realizar um experimento que irá gerar dados e você deve organizá-los em tabelas e gráficos para poder fazer um resumo dos seus resultados para a apresentação em um determinado comitê para aprovação do seu serviço. Viu como é importante entender essa questão? Gráficos bem detalhados e corretos te dão uma boa visão do que está ocorrendo em determinado setor e também é útil para mostrar à empresa as projeções.
Nos dias atuais, em qualquer apresentação empresarial, os gráficos fazem parte desse mundo, trazendo e até às vezes inovando a forma de exibir os resultados de uma empresa. Pensando nisso, seu gerente pediu sua sugestão para propor uma nova apresentação das vendas do último trimestre dos últimos 10 anos da empresa. A ideia é fazer com que esses valores fiquem apresentáveis, porém ele não tem nenhuma ideia de como fazer isso. Como você faria essa apresentação? Que tipo de gráfico você utilizaria para expor as vendas? E como você interpretaria esse gráfico?
Que tal começar esse entendimento agora? Você será acompanhado em todo o processo! Iniciaremos com os conceitos de tabelas e, depois, passaremos para os gráficos e uso do Excel!
conceito-chave
Quando falamos de dados e o que eles mostram, estamos falando de estatística, mas o que é estatística? Como podemos definir esse conceito? Em termos gerais, podemos definir estatística como um conjunto de técnicas e métodos para realização de experimentos, coleta e análise de dados (NETO, 2006). Duas ferramentas são essenciais quando trabalhamos com estatística: população e amostra.
Assimile
População: dizemos que um conjunto de elementos é uma população se tais elementos têm pelo menos uma característica em comum. Como exemplo de populações, temos árvores de uma determinada espécie, poluentes atmosféricos, pessoas que têm olhos de cor clara, etc.
Amostra: dizemos que um subconjunto de elementos é uma amostra quando ele for subconjunto de uma dada população. Como exemplo de amostra, podemos considerar um subconjunto de pessoas que têm olhos azuis da população de pessoas de olhos de cor clara.
Certo, agora que sabemos o que é uma população e uma amostra, que são as bases dos trabalhos de estatística, vamos introduzir um novo conceito que nos auxilia a construir métodos estatísticos no futuro. Esse conceito é o conceito de variável.
Assimile
Variável: dizemos que uma determinada característica é uma variável se determina a natureza de uma população e pode assumir diversas classificações de acordo com a origem da população. No planejamento da pesquisa, por exemplo, devemos definir quais são as nossas características de interesse, antes da coleta dos dados.
É importante lembrar que as variáveis, em geral, têm natureza diferente, o que nos leva à classificá-las em dois grupos: quantitativas e qualitativas. Como definimos esses conceitos? Vamos começar com as variáveis quantitativas. Tais variáveis dizem respeito a características que podem ser medidas ou contadas, por exemplo, o preço de um ativo no mercado financeiro, o número de árvores de uma determinada espécie, a taxa de hemoglobina de um paciente, etc. E as variáveis qualitativas, como definimos? Ora, como o próprio nome já diz, qualidade. Essas variáveis estão ligadas à descrição de uma característica, não podendo ser contada ou medida, mas podendo ser observada, por exemplo, o nível educacional, a cor dos olhos, o sexo de um animal, etc.
Além dessas classificações de variáveis, podemos ainda classificá-las em subcategorias. Isto é, no caso das variáveis qualitativas, podemos classificá-las em qualitativa nominal (quando não há uma ordem de classificação) ou qualitativa ordinal (quando há uma ordem de classificação). Exemplos de variáveis qualitativas nominais envolvem espécie de uma planta, cor dos olhos, sexo de um animal, etc. Já os exemplos de variáveis qualitativas ordinais envolvem a classificação do nível escolar, nível de urgência em um hospital, etc. (NETO, 2006).
Por outro lado, podemos também classificar as variáveis quantitativas em dois grupos: discretas ou contínuas. As discretas são aquelas que são originadas de um processo de contagem, como o número de peixes de uma espécie X em um determinado lago. Já as contínuas, bem, não existe uma contagem e podem assumir qualquer valor na reta real, como temperatura, índices pluviométricos, etc. (NETO, 2006).
Reflita
Como você acha que devemos representar as variáveis? É possível ter um novo tipo de classificação de uma variável?
Certo, agora que sabemos o que é uma variável e suas classificações, vamos trabalhar com a exposição de dados. Em geral, representamos os dados por tabelas de frequência, que consiste, basicamente, em listar os valores possíveis da variável, numéricos ou não, e fazer a contagem na tabela de dados brutos do número de suas ocorrências (VIRGILITO, 2017). De acordo com Magalhães (2002), são componentes de uma tabela de frequência:
- Frequência absoluta (): é o número de observações correspondente a cada classe da variável. Em geral, ela é chamada apenas de frequência.
- Frequência relativa (): é o quociente entre a frequência absoluta da classe correspondente e a soma das frequências (total observado), isto é, onde n representa o número total de observações.
- Frequência percentual (): é obtida multiplicando a frequência relativa por 100%.
- Frequência acumulada (): é o total acumulado (soma) de todas as classes anteriores até a classe atual.
Exemplificando
Suponha que uma dada variável que representa a concentração de metal no sangue (em ) de um paciente tenha como dados observados os valores: 20, 20, 20, 20, 21, 21, 21, 22, 22, 22, 22, 22, 23, 24, 24. Como representamos esses dados em tabela de frequência? Nesse caso, podemos trabalhar com a seguinte tabela de frequência:
| Concentração de metal | Número de indivíduos | % |
|---|---|---|
| 20 | 4 | 26,67 |
| 21 | 3 | 20,00 |
| 22 | 5 | 33,33 |
| 23 | 1 | 06,67 |
| 24 | 2 | 13,33 |
| Total | 15 | 100,00 |
No exemplo anterior, trabalhamos com uma representação de dados discretos. Mas como trabalhamos com dados contínuos? Nesse caso, dado que não podemos fazer uma contagem, trabalhamos com faixa de variações divididas em intervalos de classes, onde o menor valor da classe é denominado limite inferior () e o maior valor da classe é denominado limite superior () (NETO, 2006). O intervalo ou a classe podem ser representados das seguintes maneiras (MAGALHÃES, 2002):
- , onde o limite inferior da classe é incluído na contagem da frequência absoluta, mas o superior não.
- , onde o limite superior da classe é incluído na contagem, mas o inferior não.
Assim, para montar a tabela de frequência, acrescentamos uma coluna com os pontos médios de cada intervalo de classe, denotada por , que é definido como . Certo, mas como definimos a quantidade de intervalos de classe que vamos utilizar? Nesse caso, utilizamos a regra de Sturges para obter o número de intervalos de classes, isto é, , em que é o número de intervalos de classe e é o tamanho do conjunto de dados.
Exemplificando
Suponha que em uma cidade X as precipitações diárias (em mm) foram dadas por 350, 260, 390, 250, 390, 210, 400, 160, 320, 390, 230, 150, 270, 440, 500 no mês de agosto de 2020. A partir dessas observações, pela regra de Surges, vamos considerar cinco classes, uma vez que k=4,88≈5. Nesse caso, uma tabela de frequência relativa a essas precipitações diárias (em mm) da cidade é descrita por:
| Precipitação (mm) | Número de cidades | % |
|---|---|---|
| 150 ⊢ 220 | 3 | 20 |
| 220 ⊢ 290 | 4 | 26,67 |
| 290 ⊢ 360 | 2 | 13,33 |
| 360 ⊢ 430 | 4 | 26,67 |
| 430 ⊢ 500 | 2 | 13,33 |
| Total | 15 | 100 |
Entendemos então como funcionam as tabelas de frequência, vamos agora para outra ferramenta importante para a análise de dados: os gráficos. As representações gráficas de tabelas de distribuições de frequências permitem uma visualização a respeito do comportamento das variáveis, incluindo sua dispersão. Em geral, a utilização de gráficos para resumir os resultados de uma pesquisa é comum e é sempre recomendável. E já que estamos falando de gráficos, alguns pontos devem ser levados em conta na sua construção (MAGALHÃES, 2002):
- Devem ser claros, simples, atrair a atenção e inspirar confiança.
- Servem para resumir resultados importantes de uma pesquisa.
- Sempre devem ter um título completo e ser colocado na parte superior do gráfico.
- Devem ser construídos numa escala que não implique outros tipos de interpretações.
- Deve-se sempre especificar (dar nome) e graduar (criar escala) os eixos.
- Quando os dados não são próprios, deve-se citar a fonte de origem dos dados do gráfico.
Vamos então trabalhar com alguns tipos de gráficos, iniciando-se com o gráfico de barras. O gráfico de barras apresenta dados categorizados em barras retangulares em que cada barra é proporcional ao número de observações naquela categoria da variável (NETO, 2006). Utilizamos esse tipo de gráfico, em geral, para realizar comparações entre as categorias de uma variável qualitativa ou quantitativa discreta. E como fazemos esse gráfico em um software como o Excel? Ora, nesse caso, digitamos os nossos dados na planilha e vamos em Inserir > Gráficos > Barra. Como exemplo, vamos considerar o gráfico de barras feito no Excel exposto na Figura 4.1.
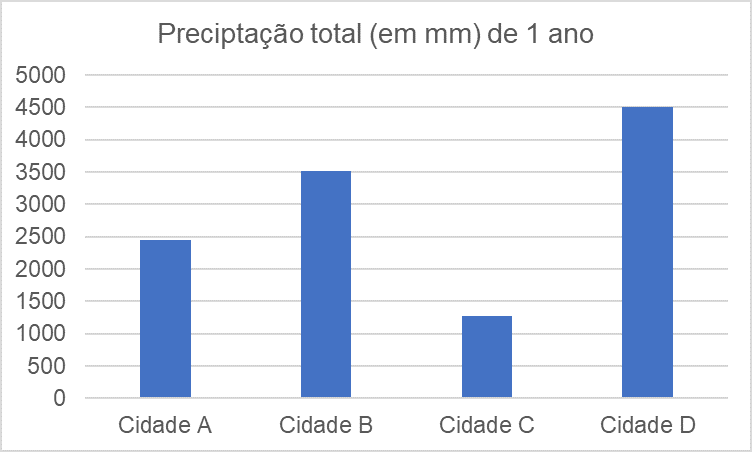
Vimos que o gráfico de barras é um gráfico para variáveis qualitativas ou variável quantitativa discreta, mas e para variável quantitativa contínua, qual gráfico utilizamos? Nesse caso, trabalhamos com o histograma, que é uma representação gráfica da distribuição de frequências em intervalos de classes de dados quantitativos contínuos. E como fazemos esse gráfico no Excel? Ora, seguimos o mesmo caminho do gráfico de barras, só mudamos o tipo de gráfico. Nesse caso, vamos na opção Inserir > Gráficos > Histograma. Como exemplo, vamos considerar o histograma feito no Excel exposto na Figura 4.2.
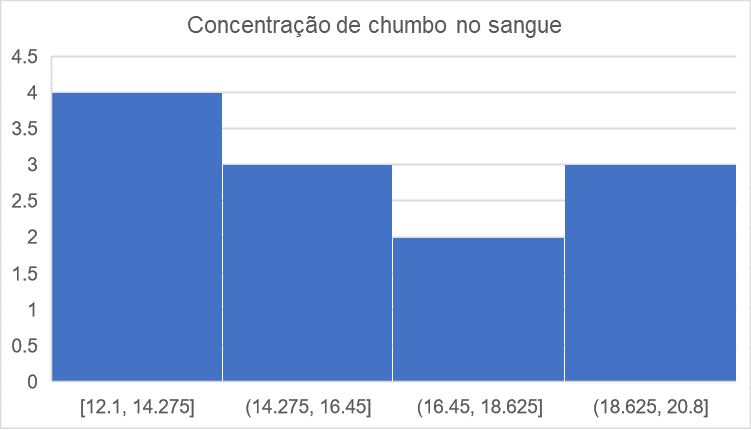
Vimos então como lidar com gráficos de barras e com o histograma. No entanto, temos um terceiro tipo de gráfico que é de suma importância para variáveis qualitativas nominais, que é o gráfico de setores. Esse tipo de gráfico é a representação gráfica da frequência relativa (percentagem) de cada categoria da variável qualitativa (NETO, 2006). E no Excel, como fazemos esse tipo de gráfico? Ora, trabalhamos como nos anteriores, Inserir > Gráfico > Pizza 2D, nesse caso. Como exemplo, vamos considerar a representação dos dados de duas espécies de plantas descritos na Tabela 4.3 a seguir.
| Plantas | Amostras | % |
|---|---|---|
| Carnívoras | 250 | 25 |
| Não carnívoras | 750 | 75 |
| Total | 1000 | 100 |
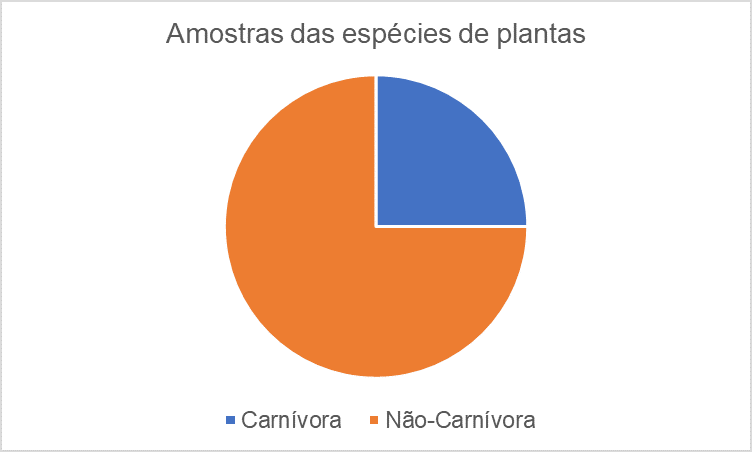
Um outro tipo de gráfico popular é o de linhas. É um tipo de gráfico que exibe informações de uma série temporal em que os valores do eixo x representam a escala de tempo e os valores do eixo y os dados observados. Os pontos são ligados por segmentos de reta (MAGALHÃES, 2002). E como fazemos no Excel? Da mesma forma que os anteriores, Inserir > Gráfico > Gráfico de linhas. Como exemplo, considere a concentração de nitrogênio no decorrer dos anos em um determinado rio, conforme a Figura 4.4.
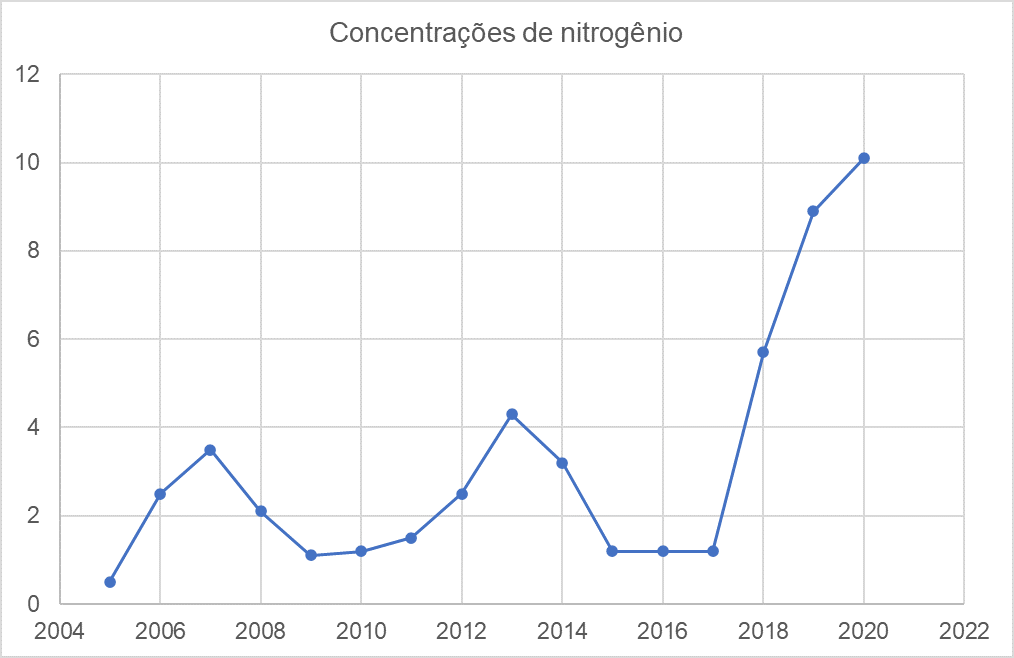
Agora, para encerrar nosso estudo de gráficos e tabelas, vamos considerar o boxplot, que é gráfico utilizado para avaliar a distribuição empírica dos dados e é extremamente comum em pesquisas médicas, por exemplo. Esse gráfico é, basicamente, formado pelo primeiro e terceiro quartil e pela mediana. No Excel, trabalhamos da mesma forma que nos anteriores, Inserir > Gráfico > Boxplot. Como exemplo, vamos trabalhar com as concentrações de chumbo no sangue de pacientes de um determinado hospital após sofrerem um acidente de trabalho em uma mina. As concentrações (em ) de cada paciente estudado são dadas por: 15.2; 10.5; 20.1; 14.2; 13.2; 15.8; 15.7; 14.2; 11.5; 17.8; 18.5. Utilizando-se o Excel, o gráfico dessa situação é dado pela Figura 4.5.
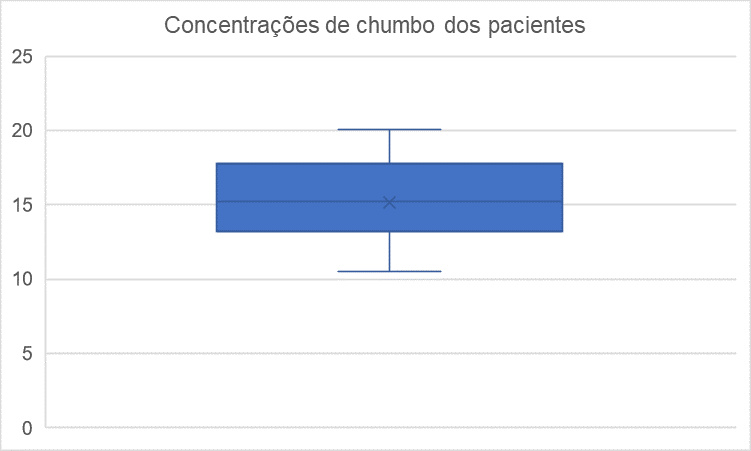
E com isso encerramos nossa seção sobre tabelas e gráficos, que são as ferramentas essenciais quando trabalhamos com estatística. Lembre-se sempre de usá-los quando você estiver atuando em sua área de trabalho!
Faça valer a pena
Questão 1
Analise o trecho a seguir:
Tipo de gráfico que exibe informações de uma série temporal em que os valores do eixo x representam a escala de tempo e os valores do eixo y os dados observados. Os pontos são ligados por segmentos de reta (MAGALHÃES, 2002).
Assinale a alternativa correta.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Correto!
De acordo com as definições de gráficos, podemos definir o gráfico de linha como sendo o tipo que exibe informações de uma série temporal em que os valores do eixo x representam a escala de tempo e os valores do eixo y os dados observados. Os pontos são ligados por segmentos de reta.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Questão 2
Suponha que você deseja avaliar as concentrações de um dado composto químico. Por rigor empresarial, você deve apresentar os resultados em forma de gráfico a partir de uma tabela de frequência dividida em intervalos de classe e assumindo que os dados são exposto em escala contínua.
Com base nos tipos de gráficos, assinale a alternativa correta.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Correto!
De acordo com as definições de gráficos e tabelas, como temos intervalos de classe e uma escala contínua, o gráfico mais adequado para a situação é o histograma, que trabalha com a representação gráfica dos intervalos de classe.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Questão 3
Suponha que as concentrações de sódio em um determinado alimento produzido anualmente sejam descritas pelo seguinte gráfico de linhas exposto na Figura 4.8.
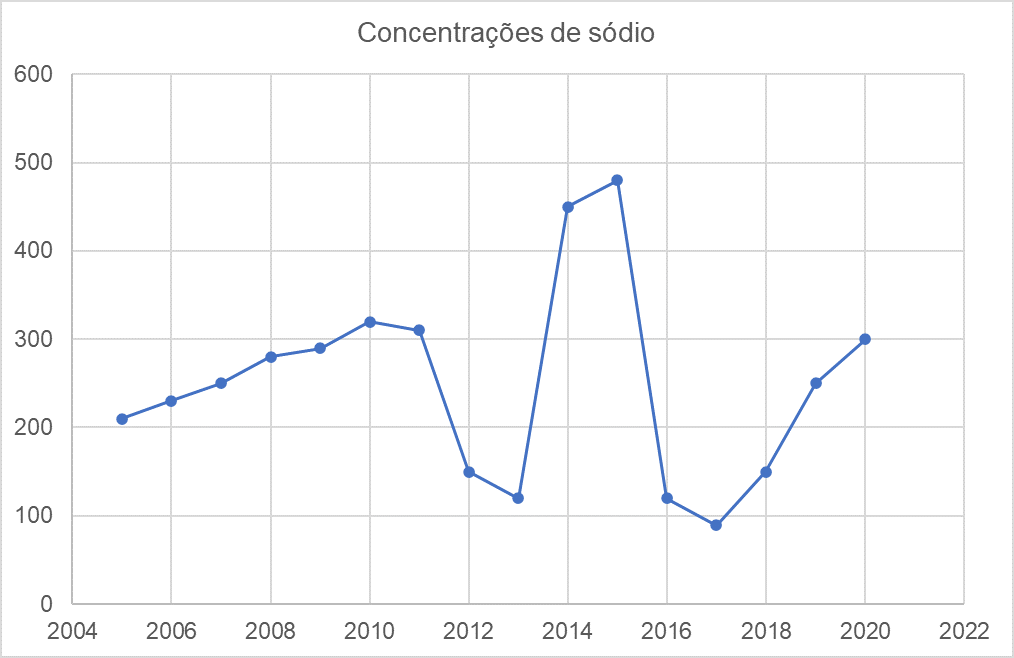
Suponha também que nos interessa saber como interpretar esse gráfico para tirar conclusões acerca do sódio desse alimento em anos diferentes da sua produção.
Assinale a alternativa correta.
Correto!
Analisando o gráfico, concluímos que no período entre 2013 e 2015 houve uma alta da concentração de sódio no alimento, atingindo o pico máximo em 2015. Entre 2015 e 2017, houve uma queda da concentração de sódio, tendo-se como mínimo o valor de concentração em 2017.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Referências
HENRIQUES, C. Análise de regressão linear simples e múltipla. Departamento de Matemática. Escola Superior de Tecnologia de Viseu. Portugal, 2011.
JUNIOR, P. J. R. Introdução ao Ambiente Estatístico R. In: JUNIOR, P. J. R. Gráficos no R. Universidade Federal do Paraná, Curitiba, 2011. Disponível em: http://www.leg.ufpr.br/~paulojus/embrapa/Rembrapa/Rembrapase9.html. Acesso em: 13 abr. 2021.
MAGALHÃES, M. N.; LIMA, A. C. P. Noções de probabilidade e estatística. São Paulo: Editora da Universidade de São Paulo, 2002.
NETO, P. L. O. C. Estatística. São Paulo: Blucher, 2006.
THE R Project for Statistical Computing. Disponível em: https://www.r-project.org. Acesso em: 12 abr. 2021.
VIRGILITO, S. B. Estatística Aplicada. São Paulo: Saraiva, 2017.



