lorem ipsum dolor sit amet
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nunc dignissim euismod urna tincidunt sagittis. Vivamus id vehicula eros, non scelerisque eros.

Fonte: Shutterstock.
Deseja ouvir este material?
Áudio disponível no material digital.
Praticar para aprender
Caro aluno, nesta seção iremos entender os conceitos de dispersão, correlação e regressão. Com esses conceitos em mente, você entenderá que boa parte dos resultados é baseada nesses conceitos. Como exemplo dessa abordagem, você pode considerar um estudo que deseja avaliar a resistência de uma viga de acordo com o tipo de material. Para atingir tal objetivo, você irá trabalhar com o que chamamos de modelo de regressão, que lhe trará todas as conclusões necessárias a respeito do seu experimento com as vigas, permitindo um melhor entendimento e a interpretação do experimento em questão.
Suponha que você, um engenheiro ambiental com especialidade em poluição atmosférica, decida trabalhar com análise da qualidade do ar. Como você ainda está iniciando nessa área, decidiu utilizar um banco de dados de prática chamado “airquality” do software R, cujas primeiras linhas são:
Ozone Solar.R Wind Temp Month Day
1 41 190 7.4 67 5 1
2 36 118 8.0 72 5 2
3 12 149 12.6 74 5 3
4 18 313 11.5 62 5 4
5 NA NA 14.3 56 5 5
6 28 NA 14.9 66 5 6
Para trabalhar com esses dados, você necessita de um modelo de regressão. Assumindo que a variável resposta, Y, seja a concentração de ôzonio, qual modelo de regressão você montaria? Como você estima os parâmetros desse modelo? E as interpretações desses parâmetros, como faria?
Que tal começar esse entendimento agora? Você será acompanhado em todo o processo! Iniciaremos com os conceitos de dispersão e correlação, que são necessários para a construção do modelo de regressão, objetivo principal desta seção!
conceito-chave
Você já parou para pensar em como podemos visualizar a relação entre dados? Não? Ora, para isso, podemos utilizar diagramas de dispersão. Mas o que é um diagrama de dispersão? Podemos dizer que diagrama ou gráfico de dispersão é uma ferramenta estatística que indica a existência, ou não, de relações entre variáveis. Em geral, esse tipo de gráfico é utilizado quando desejamos saber o que acontece com uma variável quando a outra se altera, como uma espécie de causa e efeito.
Por exemplo, um engenheiro mecânico deseja avaliar o consumo de combustível (milhas por galão) de carros de acordo com o tipo de transmissão (automática ou manual). Em geral, acredita-se que o tipo de transmissão causa um maior consumo de combustível, especialmente se o carro for automático. Mas será que isso é verdade? Vamos verificar o diagrama de dispersão (Figura 3.1) para ver o que acontece.
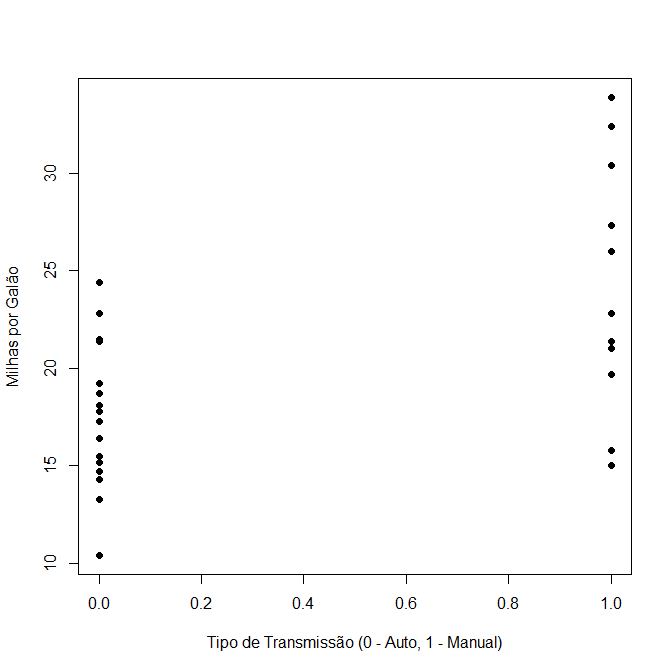
Baseando-se nesse diagrama, podemos observar dois fatos. O primeiro, as milhas por galão dos carros automáticos parecem estar todas próximas ao mesmo limiar e menos dispersas quando comparadas aos carros manuais. O segundo fato é que alguns dos carros manuais analisados parecem tem um consumo duas vezes menor do que alguns carros automáticos.
Assim, podemos concluir que, sem nenhum tipo de inferência estatística, os carros manuais parecem ser mais econômicos. É claro que somente o tipo de transmissão não é suficiente para determinar o consumo, isto é, precisamos de uma análise mais detalhada para tal. Esse exemplo serve para reforçar que devemos ter muito cuidado ao analisar informações, dado que muitas delas são necessárias para chegar a uma conclusão e não apenas um olhar superficial, considerando o mínimo de informações.
Uma outra medida importante sobre relação entre variáveis é o coeficiente de correlação. Em 1896, Karl Pearson propôs o tão famoso coeficiente de correlação ρ (ou produto-momento) de Pearson. Esse coeficiente tem por objetivo estudar a relação entre duas variáveis e tem como vantagem ser um número puro, isto é, não tem uma unidade de medida definida.
Para trabalhar com esse coeficiente, considere as observações de uma variável X (por exemplo, milhas por galão) e as observações de uma variável Y (por exemplo, cilindradas de um motor). Sendo e , respectivamente, as médias e os desvios-padrão amostrais de ambas as variáveis, podemos escrever o coeficiente da correlação de Pearson da seguinte forma:
em que
representa a covariância entre e .
Dessa equação, tiramos as duas principais propriedades do coeficiente de correlação: o sinal e a magnitude. O sinal se relaciona com o tipo de relacionamento: crescente (sinal positivo) e decrescente (sinal negativo). Quando se estuda a relação entre duas ou mais variáveis, é importante levar em conta essa informação, pois ela nos diz, por exemplo, se X está crescendo, então Y está decrescendo ou crescendo, dependendo do sinal. Por exemplo, considerando carros, se tivemos um aumento nas cilindradas, espera-se que o veículo gaste mais combustível e consequentemente fará menos milhas por galão. Mas como verificamos essa informação? Inicialmente com o coeficiente de correlação.
Por outro lado, a magnitude do coeficiente de correlação varia no intervalo de (-1,1) e indica, no gráfico de dispersão, um formato visual mais próximo de uma reta. Por exemplo, valores próximos de -1 indicam uma correlação negativa perfeita (praticamente uma reta decrescente), e valores próximos de +1 indicam uma correlação positiva perfeita (praticamente uma reta crescente). Em ambos os casos, a dispersão dos dados é extremamente baixa, o que é desejável em quase todos os tipos de análises estatísticas. Além disso, temos o caso em que a magnitude é igual a 0, que nos indica que não há, no gráfico de dispersão, uma forma definida e os dados se apresentam mais dispersos mostrando que as variáveis podem não ter nenhum tipo de relação.
Certo, entendemos o que é coeficiente de correlação e também o que é gráfico de dispersão, mas ainda falta um certo conceito que vai nos dar um norte para nosso objetivo principal dessa seção: o modelo de regressão linear. Mas então, qual é o conceito restante? Ora, é o que chamamos de coeficiente de determinação , que é simplesmente definido como sendo , isto é, o coeficiente de determinação é o quadrado do coeficiente de correlação. Esse coeficiente é útil, em particular, para explicar a proporção da nossa variável resposta, dada a variabilidade das outras variáveis, chamadas de preditoras.
Vamos a um exemplo prático de como interpretamos esse coeficiente. Para isso, suponha que ao avaliar a correlação entre as variáveis Y = “milhas por galão” e X = “cilindradas do veículo”, obtivemos um valor para o coeficiente de correção. Nesse caso, a partir da definição do coeficiente de determinação, temos que ou 62%. Mas o que isso quer dizer? Ora, dizemos que cerca de 62% da variabilidade da variável Y é explicada pela variável X, isto é, 62% da variação de consumo é explicado pelas cilindradas do veículo e vice-versa. Em geral, procuramos sempre por um coeficiente de determinação superior a 90% para uma melhor interpretação, porém isso nem sempre é possível, como vimos nesse exemplo.
Assimile
Esta é uma frase importante que devemos ter em mente: não é porque duas variáveis estão relacionadas que uma é a causa da outra. Por exemplo, vamos considerar o número de pessoas que praticam esporte, tipo corrida, e a quantidade de suplementos esportivos consumidos são altamente correlacionados. Porém, isso não significa que a prática de corrida causa necessariamente a compra de suplementos esportivos. Em geral, é complicado estabelecer relações causais considerando apenas dados observacionais, é necessário também a realização de experimentos para essa finalidade.
Agora temos todas as ferramentas para o prato principal da nossa seção: o modelo de regressão linear. Mas antes, vamos entender a origem desse modelo. Em um estudo para trabalhar a relação entre a altura dos pais e dos filhos ( e ), a fim de verificar como a altura do pai influenciava a altura do filho, Galton deu origem, no século XIX, ao que conhecemos hoje como teoria de regressão. O termo regressão veio pelo fato de que no experimento de Galton as medidas estudadas tendiam a regredir à média. De modo geral, os modelos de regressão têm como objetivos:
- Predição – consiste em predizer valores de Y por meio de valores de X não presentes entre os dados originais. Isto é, trabalhamos com possíveis valores de X e obtemos valores de Y, desde que boa parte da variabilidade de Y seja, de fato, explicada por X.
- Seleção de variáveis – consiste em selecionar as variáveis que têm algum impacto significante em relação à variável de interesse (variável resposta).
- Estimação de parâmetros – encontrar valores que são utilizados para inferir resultados sobre os parâmetros da população, por exemplo, cálculo de doses letais, tempo até a cura de uma doença, porcentagem de falha de uma máquina industrial, etc.
- Inferência – após encontrar os valores dos parâmetros, o processo de inferência serve para discutir/inferir resultados sobre uma dada população e estabelecer critérios como intervalo de confiança sobre tais resultados.
No que tange aos modelos de regressão, algumas nomenclaturas são importantes. Por exemplo, as variáveis Xs são chamadas variáveis independentes ou explanatórias, enquanto que a variável Y é chamada de variável dependente ou resposta. Com esses nomes em mãos, vamos estabelecer o modelo de regressão linear simples. Suponha que a relação verdadeira entre X e Y pode ser escrita pode uma equação de reta. Então, o valor esperado de Y para cada valor de X é dado por:
sendo que os parâmetros da equação da reta e são constantes desconhecidas. Quando X = 0, representa o ponto onde a reta corta o eixo dos Ys. Esse parâmetro é chamado de intercepto. Por outro lado, é chamado coeficiente de regressão ou declive da reta e ter interpretação descrita como “a cada aumento de 1 unidade em X, temos que aumenta unidades”.
Agora, dados , se for admitido que Y é uma função linear de X, o modelo de regressão linear simples é dado por:
sendo e os parâmetros do modelo e é o erro aleatório do modelo. Alguns pressupostos desse modelo devem ser levados em consideração (HENRIQUES, 2011):
(i) A relação entre Y e X é linear.
(ii) A média do erro aleatório é nula, isto é, .
(iii) Para um dado valor de X, a variância do erro é sempre , isto é, , o que implica que .
(iv) O erro de uma observação é independente do erro de outra observação, isto é, .
(v) Os erros têm distribuição normal, isto é, e, portanto, .
Agora nosso problema é, necessariamente, estimar os parâmetros e do modelo. Para isso, trabalhamos com o método dos mínimos quadrados, que é baseado em um minimizar o comprimento do vetor . Pela definição da norma Euclidiana, temos que:
Deseja-se, portanto, estimar e , tal que Z seja mínimo. Esse método é chamado método dos mínimos quadrados. Para isso, obtém-se as derivadas parciais:
Igualando ambas as derivadas a zero, obtemos as equações normais:
.
de onde tiramos que . Por outro lado, substituindo a expressão de no sistema das equações normais, obtemos que o estimador de é dado por:
Exemplificando
Para exemplificar como se utiliza o modelo de regressão, vamos considerar um exemplo em que Y = “Milhas por Galão (mpg)” e X = “Peso do Veículo”, em que nosso objetivo é verificar se X causa influência em Y. Os dados desse exemplo se encontram disponível no software R com o nome de “mtcars”.
Inicialmente, vamos trabalhar com o diagrama de dispersão. Nesse caso, de acordo com a Figura 3.2, podemos observar que há uma tendência aparentemente linear e negativa, o que indica que o coeficiente de correlação está próximo de -1. Fazendo os cálculos da correção, obtemos que ela é dada por , que implica em um coeficiente de determinação igual a , isto é, cerca de 75% da variabilidade de Y é explicada por X.
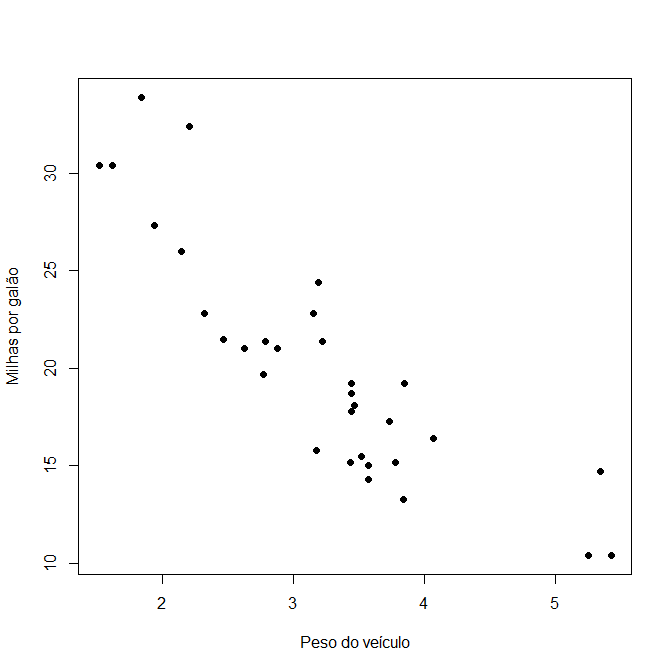
Vamos ao modelo de regressão. Sabemos que:
e
Realizando os cálculos, temos:
Declive - indica que, em cada unidade em que o peso aumenta, as milhas por galão do veículo reduzem, em média, 5,3445 mpg.
Ordenada na origem - . Nesse caso, temos que quando o peso do veículo é igual a zero, as milhas por galão são, em média, 37,2851 mpg. Perceba que essa interpretação, na prática, é impossível de acontecer dado que qualquer veículo tem um peso mínimo. Essa impossibilidade nos mostra que, na ausência de mais informação, a validade de uma relação linear não pode ser extrapolada para longe dos valores observados de .
E com isso encerramos nossa seção sobre análise de regressão, viu como é importante essa ferramenta? Deixo também como encerramento a seguinte reflexão.
Reflita
Como você trabalharia com análise de regressão na sua área de trabalho? Qual software você utilizaria? Conhece algum?
Faça valer a pena
Questão 1
Quando falamos de análise de regressão, precisamos entender quais são os objetivos de uma regressão linear, isto é, com que finalidade usamos um modelo de regressão linear. Caso não saíbamos o que seja isso, o uso deve perder sua essência.
Com base nos objetivos de um modelo de regressão linear, assinale a alternativa correta.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Correto!
Por definição, um modelo de regressão linear tem por objetivos:
Predição: consiste em predizer valores de Y por meio de valores de X não presentes entre os dados originais. Isto é, trabalhamos com possíveis valores de X e obtemos valores de Y, desde que boa parte da variabilidade de Y seja, de fato, explicada por X.
Seleção de variáveis: consiste em selecionar as variáveis que têm algum impacto significante em relação à variável de interesse (variável resposta).
Estimação de parâmetros: encontrar valores que são utilizados para inferir resultados sobre os parâmetros da população, por exemplo, cálculo de doses letais, tempo até a cura de uma doença, porcentagem de falha de uma máquina industrial, etc.
Inferência: após encontrar os valores dos parâmetros, o processo de inferência serve para discutir/inferir resultados sobre uma dada população e estabelecer critérios como intervalo de confiança sobre tais resultados.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Questão 2
Suponha que ao avaliar um modelo de regressão a respeito das variáveis Y = {produção de uvas} e X = {taxa de irrigação}, você se deparou com coeficiente de determinação de . A partir desse coeficiente, deseja-se conhecer sua interpretação e também o coeficiente de correlação entre as variáveis.
Com base na definição de coeficiente de correlação, assinale a alternativa correta.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Correto!
O coeficiente de determinação é simplesmente definido como sendo , isto é, o coeficiente de determinação é o quadrado do coeficiente de correlação. Assim, considerando os dados do exercício, concluímos que . Logo, podemos fazer a seguinte interpretação: “O coeficiente de determinação igual a 0,97 indica que 97% da variabilidade da produção de uvas é explicada pela taxa de irrigação. Além disso, o coeficiente de correlação entre as variáveis é de 0,984, que indica uma correlação positiva e forte entre a produção de uva e a taxa de irrigação”.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Questão 3
Suponha que Y seja uma variável relacionada com velocidade e X uma variável relacionada com distância percorrida. Foi admitido um modelo de regressão linear os dados gerados por essas variáveis, tal que , , e .
Com base no conceito de análise de regressão linear simples, assinale a alternativa que contém o valor de e sua interpretação.
Correto!
Sabemos que:
e
Realizando os cálculos, temos que: . A interpretação desse valor é descrita como: “quando a distância percorrida está no marco zero quilômetro, a velocidade do veículo é de 8,2839 km/h”.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Tente novamente...
Esta alternativa está incorreta, leia novamente a questão e reflita sobre o conteúdo para tentar outra vez.
Referências
AMARAL, G. D.; SILVA, V. L.; REIS, E. A. Análise de Regressão Linear no Pacote R. Relatório Técnico Série Ensino RTE 001/2009. Universidade Federal de Minas Gerais, Belo Horizonte, 2009. Disponível em: http://www.est.ufmg.br/portal/arquivos/rts/RT-SE-2009.pdf. Acesso em: 12 abr. 2021.
HENRIQUES, C. Análise de regressão linear simples e múltipla. Departamento de Matemática. Escola Superior de Tecnologia de Viseu. Portugal, 2011.
MAGALHÃES, M. N.; LIMA, A. C. P. Noções de probabilidade e estatística. Editora da Universidade de São Paulo, 2002.
NETO, P. L. O. C. Estatística. São Paulo: Blucher, 2006.
THE R Project for Statistical Computing. Disponível em: https://www.r-project.org. Acesso em: 12 abr. 2021.
VIRGILITO, S. B. Estatística Aplicada. São Paulo: Saraiva, 2017.



